Näin villin pörssiviikon jälkeen mielessä saattaapi pyöriä riskinhallinnallisia kysymyksiä. Kuinka paljon pitäisi laittaa kiinni houkuttelevaan sijoituskohteeseen? Entä kuinka suuret omaisuuserät olisi syytä vakuuttaa? Seuraavassa tullaan huomaamaan, että vastaus ei ole sama yhden henkilön elämän polulla ja usean henkilön joukolle. Samalla tulee havainnollistettua matemaattinen käsite ergodisuus.
Kolikon heittoa
Lähdetään liikkelle yksinkertaisesta vedonlyönnistä. Varakas kaverisi tarjoaa mahdollisuutta pelata tasapainoisella kolikolla peliä, jossa arvaamalla kolikon puolen oikein voitat 2.11 kertaa panoksesi verran. Aikaa on pelata peliä 100 kertaa. Vedon odotettu tuottoprosentti (p * k = 0.5 * 2.11 = 1.055 = 105.5% ) on suurempaa kuin 100% joten veto kannattaa ottaa vastaan, mutta kuinka suuri osuus omaisuudesta siihen kannattaa sijoittaa yhdelle kierrokselle? Vastaa tähän vastaus intuitiivisesti ennen kun jatkat eteenpäin.
Lähdetäänpä sopivaa panoskokoa fiilispohjalta haarukoimaan. Koko varallisuuden menettäminen 50% todennäköisyydellä heti kättelyssä ei lämmitä mieltä, joten kaikkea ei laiteta peliin. Kuinkas olisi puolet varallisuudesta? Jos alkuun sattuisi tulemaan vaikka 3 tappion putki ja joka kerta löisimme sisään puolet varoista, olisi jäljellä enää 12.5% varoista. Sieltä nouseminen takaisin ylös olisi hyvin hikinen urakka, joten fiilispohjalta jo osaamme pudottaa panosta pienemmäksi. Voisiko 20% olla sopiva? Lähdetään sitä tutkimaan tarkemmin. Katsotaan kuinka kävisi 1000€ varallisuudelle kahden vedon jälkeen, mikäli tuurit olisivat odotetut eli tulisi yksi voitto ja yksi tappio. Järjestyksellä ei ole väliä, mutta kirjoitetaan kaava niin että ensi tulee tulee voitto ja sitten tappio.
(1+1.11*0.2) * (1-0.2) * 1000 € = 977.6€
Siis hetkinen, vedon tuotto-odotus piti olla voitollinen ja silti saldo on tappiolla vaikka tuurit meni tasan. Kyseessä ei ole musta magia vaan liian suuri panostus omaan varallisuuteen nähden. Pudotetaan panostustaso vielä reilusti alaspäin 5%:iin. Nyt vastaava laskelma menee.
(1+1.11*0.05) * (1-0.05) * 1000 € = 1002.7€
Vihdoinkin voiton puolella. Viisi prosenttia varallisuudesta vaikuttaisi ainakin turvalliselta panostustasolta tähän vedonlyöntiin. Kellyn kriteerillä (pohjautuu tähän informaatioteorian tutkimukseen) pystymme optimoimaan vedonlyönnin panostustasoa omaan varallisuuteen sopivaksi. Tällaisessa yksinkertaisessa tapauksessa optimaalinen panostaso voidaan laskea kaavalla odotettu_tuotto / (kerroin-1), mikä on nyt 0.055 / 1.11 = 0.05. Aiemmin turvalliseksi veikattttu 5% panostustaso on myös Kellyn kriteerillä optimaalinen.
Arviodaan sitten, mitä tapahtuisi 100 heiton jälkeen, mikäli kaikki menisi odotetusti, eli 50 kertaa arvataan oikein ja 50 kertaa väärin. Järjetyksellä ei edelleenkään ole merkitystä koska kyse on kertolaskuista. Alla olevassa kuvaajassa on kuvattu lopputulemat riippuen panostasosta. Käyrän huippu on Kellyn kriteerillä optimoitu 5% varallisuudesta ja kaikki yli 10% panostukset johtavat tappioihin. Mikäli vedonlyöntiä jatkettaisiin vielä 100 toiston jälkeenkin, yli 10% panostus tulisi johtamaan vararikkoon. Ennemmin tai myöhemmmin.
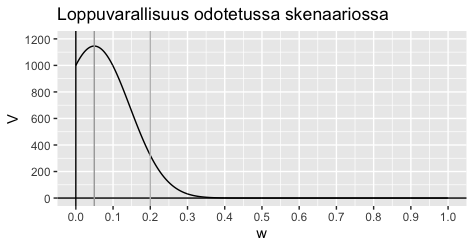
Nyt joukolla kolikkoa heittämään
Entäpä jos emme pelaisikaan yksinään 100 kertaa vaan 99 kaverin kanssa pelaisimme jokainen kerran? Jokaisella sadalla ryhmän jäsenellä on sama 1000 euron varallisuus alussa ja tavoitteena on joukkueena jäädä mahdollisimman paljon voitolle. Nyt odotetussa skenaariossa (50 voittajaa ja 50 häviäjää) ryhmän keskimääräinen loppuvarallisuus olisi 20% panostuksella seuraava:
(50 * (1 + 0.2 * 1.11) * 1000 € + 50 * 0.8 * 1000€) / 100 = 1011€.
Keskimäärin ryhmä teki voittoa ja tässä tilanteessa 20% ei vaikuta enää niin vaaralliselta panostasolta. Vaikka tulisi alkuun tappioputki, pääsevät sen jälkeen ryhmän jäsenet liikkeelle aina alkuperäisellä 1000€ varallisuudella. Vastaavasti voidaan laskea, kuinka kävisi 5% panostuksella.
(50 * (1 + 0.05 * 1.11) * 1000 € + 50 * 0.95 * 1000€) / 100 = 1002.75€
Tämäkin on voiton puolella. Mielenkiintoista tässä kohtaa on kuitenkin se, että keskimääräinen voitto on nyt huomattavasti pienempi kuin samalla panostustasolla yhden henkilön sadalla toistolla. Yllä olevasta kuvaajasta nähtiin, että silloin päädytään n. 1145€ voittoon. Mistähän tämä ero johtuu?
Vastaus on korkoa korolle ilmiö. Panoskoko 5% on yhden hengen sadalle toistolle turvallinen ja varallisuuden pikkuhiljaa kasvaessa aiemmat voitotkin kasvavat korkoa. Ryhmässä, jossa jokainen aloittaa aina ”alusta” tätä efektiä ei pääse syntymään ja paras taktiikka on panostaa agressiivisesti.
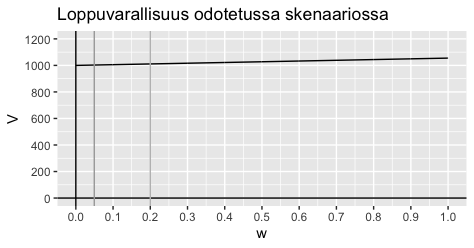
Keskimääräisen loppuvarallisuuden (V) arvoja suhteellisen panoskoon (w) funktiona odotetussa 100 kolikonheiton sarjassa. 100 pelaajaa pelaa kerran.
Ryhmätilanteessa yksittäisten henkilöiden konkurssitkaan eivät tuo niin merkittävää haittaa koska vain joukkueen menestyksellä on väliä. Käytännössä siis joukkue jakaa voittopotin lopuksi kaikkien kesken. Yhden henkilön yhdessä sarjassa konkurssi taas on katastrofi: kaikki meni ja peli loppui siihen. Ylös ei ole nousua ennen kun on taas palkkapussista uuden alkupääoman säästänyt.
Ergodisuus
Kolikonheittoesimerkki on monella tapaa yksinkertainen. Siinä ei ole esim. huomioitu, että sadassa toistossa ei lopputulos läheskään aina ole 50-50 vaan satunnaisuudella on iso rooli. Se kuintenkin havainnollistaa sitä että vedonlyönti / sijoittaminen ei ole ergodinen ilmiö. Ilmiö olisi ergodinen, mikäli sen ajallisten toistojen odotusarvo on sama kuin usean yhtäaikaa tapahtuvan toiston odotusarvo. Nyt nähtiin, että vedonlyönnissä ajalliset toistot on kerrannaisilmiö ja ryhmävedonlyönti summautuva ilmiö ja täten riskien hallinta aivan erilaista. Mikäli ergodisuus ilmiönä yleisesti kiinnostaa enemmän, kannattaa lukaista Ole Petersin vasta julkaistu artikkeli The ergodicity problem in economics. Me mennään eteenpäin vielä parilla esimerkillä.

Vakuutukset
Missäs muualla kuin kolikonheitossa ergodisuutta voisi pohtia? Eräs esimerkki on vakuutus. Alkuun voidaan faktana todeta, että ryhmänä kaikille vakuutusyhtiön asiakkaille vakuutusten ottaminen ei ole järkevää. Vakuutusyhtiöt maksavat palkkaa työntekijöilleen ja silti tuppaavat tekemään pientä voittoakin vakuutusmaksujen avulla korvausten jälkeen. Tämäkkään ilmiö ei ole enää niin yksioikoinen kun tutkitaan asiaa yksilön kannalta.
Olkoon meillä asuinrakennus, jonka arvo on 50 000€. Rakennukselle on vakuutus, joka maksaa vuodessa 100€. Yksinkertaistetaan mahdollisia vahinkoja sen verran että pienet vahingot jätetään pois vakuutuksen piiristä. Vahinko toteutuessaan tuhoaa koko asunnon ja vahingon todennäköisyys on 0.1% yhden vuoden aikana. Voidaan ajatella, että yhtenä vuonna vakuutusmaksun maksamatta jättäminen on veto, jolla asiakas voittaa 100€ 99.9% todennäköisyydellä, ja häviää 50000€ 0.1% todennäköisyydellä. Vakuutusyhtiö, jolla on paljon asiakkaita eli lukuisia rinnakkaisia vetoja, toivoo, että asiakas maksaa vakuutusmaksun, koska firma tekee silloin odotusarvoisesti voittoa n. 50€.
Asiakkaan kannalta vedon järkevyys riippuu hänen varallisuudestaan. Vedon (= ei maksa vakuutusmaksua) kerroin on nyt 1.002 ja osumistodennäköisyys 99.9%. Kellyn kriteeri suosittaa tällaiseen vetoon sijoittamaan 50% varallisuudesta. Asiakkaalla tulisi siis olla varallisuutta vähintään 100 000€ , jotta hän pystyy tällaista 50 000€ riskiä ottamaan. Mikäli taas asunnossa on kiinni yli puolet omaisuudesta, riskin karttaminen ja vakuutusmaksun maksaminen on varsin perusteltua. Tässäkin jäi vielä huomiotta ihmisten erilaiset henkiset kapasiteet riskinottoon (ekonomistikielellä riskiaversio), mikä helposti johtaisi vieläkin varovaisempaan toimintaan.
Osakesijoittaminen
Osakesijoittamista tulee ajatella aivan samoin yhtenä pitkittäisenä prosessina samoin kuin yhden henkilön vedonlyöntiä. Sen matemaattisesta kuvaamisesta tekee hankalaa se että yhden ”vedon”, esimerkiksi osakkeen markkina-arvon vuosimuutoksen, lopputulemia on lukuisia erilaisia. Kolikonheitossa päästiin helpolla, koska vaihtoehtoja on vain osuma ja huti. Kolikonheitossa myös osumisen todennäköisyys tiedettiin olevan tarkalleen 50% kun taas sijoittamisessa tulevaisuuden skenaarioiden todennäköisyyksien arviointiin liittyy huomattavaa epävarmuutta. Näitä ongelmia yritän parhaillaan taklata kun teen kauppatieteiden gradua tästä aiheesta. Toivottavasti ensi kesänä osaan kertoa aiheesta enemmän.
Loppusanat
Kuinka suuri katastrofi rahallinen konkurssi lopulta on? Ainakin rikosrekisteri- ja luottotietomerkintöjä pitäisi välttää viimeiseen asti, koska ne seuraavat taakkana pitkään elämässä. Pienen omaisuuden menettäminen nuorena, kun on vielä vastuussa vain itsestään, ei ole mikään lopullinen turmio ainakaan Suomen kaltaisessa hyvinvointivaltiossa. Itselläkin tuli näin jälkikäteen pohdiskeltuna pelattua nuorena pokeria välillä turhan reippailla panoksilla pelikassaani nähden. Nykyään taas perheen isänä oma konkurssi näkyisi myös perheenjäsenten elämässä ja riskinhallinta-asioihin suhtaudun aivan erilaisella vakavuudella.
Tästä kirjoituksesta toivon sen jäävän käteen, että ihminen jolla on vain yksi elämä täytyy harjoittaa erilaista riskienhallintaa kuin kissa, jolla on 9 elämää. Konkurssissa peli tuppaa pysähtymään. Sopivan pienet riskit kuitenkin mahdollistavat korkoa korolle kasvun. Niin varallisuudessa kuin osaamisessa.

Mielenkiintoinen tapa käyttää tilastotiedettä arkielämän asioiden miettimisessä. Pitää lukea muitakin postauksiasi.
Kiitoksia! Kyllähän täältä monenlaisia rustauksia löytyy. Toivottavasti eivät tuota pahoja pettymyksiä.
Olipa aihetta valaiseva postaus, kiitos! Kategoroiden ja avainsanapilven perusteella pitää kaivella muitakin postauksiasi, mielenkiintoisia aiheita käsittelet ja kirjoitat niistä niin, että noviisimpikin lukija pysyy mukana.
Fysiikkaa ja matematiikkaa opiskelleiden kavereiden kanssa olemme monesti puhuneet todennäköisyyslaskelmista erityisesti nopan heittämisessä (pelaamme siis perinteisiä pöytäroolipelejä). Miten esimerkiksi konkreettisen, fyysisen nopan heittämisen todennäköisyydet eroavat tietokoneella generoidusta numerosta?
Näiden asioiden pohdiskelun lukeminen kyllä kiinnostaa, kun itselläni nimenomaan se todennäköisyydet ja tilastot -kurssi oli lukion matemattikassa se haasteellisin. Mutta tästä tuli hienoa asiantuntijaperspektiiviä.
Kiva kuulla. Sinua saattaisi kiinnostaa myös vanha Kimblen nopan todennäköisyyksiin liittyvä kirjoitus
https://statistition.com/?p=440
ja ehkä jopa vielä syvällisemmin satunnaisuutta pohdiskeleva tosi vanha kirjoitus :)
https://statistition.com/?p=117
[…] urheiluvedonlyöjänä Kellyn kriteeristä on muodostunut standardi riskinhallinan työkalu. Tässä kirjoituksessa aiemmin jo avasin Kellyn kriteerin saloja yksinkertaisessa vedonlyönnissä. Lyhyesti tavoitteena […]