Oma kirjojen lukemisharrastukseni alkoi lapsena salapoliisikirjoilla. Ainakin Neiti Etsivä ja 3 Etsivää -sarjat olivat kovaa kamaa. Idolin asemaan nousseita rosmon jahtaajia olivat myös esim. Ihmemies MacGyver sekä vielä ihmeellisempi Superhessu. Erilaisten mysteerien ratkaiseminen on kiehtonut läpi elämän ja aikuisena mm. Dan Brownin kirjat ovat maistuneet.
Urani ei ole johtanut poliisiopistoon, mutta oikeiden ”rikosmysteerien” selvittelyn makuun olen vihdoin päässyt tullessani kahden lapsen isäksi. Seuraavassa kerron tositapahtumiin perustuvan tarinan kuinka todennköisyyslaskenta tuli apuun arjen mysteerin ratkaisemisessa.

Tarina isä etsivästä
Eräänä talvisena päivänä sisarukset, tyttö 1 v. ja poika 2.5 v., ovat kahdestaan leikkimässä samassa huoneessa. Yhtäkkiä talon täyttää karmaiseva tytön rääkäisy. Viereisessä huoneessa maailman menoa pohdiskellut isä ryntää paikalle ja huomaa kaksi lastaan istuvan vierekkäin. Tytöllä on jalat paljaana ja toisessa jalkapöydässä komeilee hailakat, mutta selvästi havaittavat tuoreet hampaan jäljet. Vieressä istuva, vielä heikonlaisesti sanoja muodostava, poika toistaa yhtä sanaa: ”hampaat”.
Poikaa on jo aiemmin päivällä varoitettu sisarensa tönimisestä ja muusta kiusaamisesta, joten ensimmäinen ajatus isällä on: ”Nyt lähti poika kunnon puhutteluun ja toiseen huoneeseen joksikin aikaa.” Jostain mielen syövereistä tulee hänelle kuitenkin signaali laittaa jarrut päälle, koska onhan täällä toinenkin epäilty: tyttö itse. Hetken tilannetta tutkittuaan, mikään johtolanka ei auta syyllisen valitsemisessa. Puremisjälki on sen verran hailakka, ettei siitä pystynyt päättelemään syyllistä esim. hampaiden koon perusteella. Niinpä isä päättää noudattaa länsimaista oikeusperiaatetta tuomitsematta ketään ilman painavia todisteita ja tyytyi vain lohduttelemaan vieläkin hieman itkua tihrustavaa tyttöään.
Asia jää kuitenkin hieman isää kolkuttelemaan. ”Käytinkö sittenkään hyväkseni kaikkea tietoa mysteerin arviointiin? Mikähän on todennäköisyys, että poika on sittenkin syyllinen tapahtuneeseen?” Tilanne kärjistyy isän päässä niin radikaalisti, että hän päättää ottaa esille taikakalunsa, kynän ja sanomalehden reunan, ja alkaa rapsuttelemaan mysteeriä. Hän päätyy jakamaan puremistapahtuman kahteen vaiheeseen:
- Tytön jalan laittaminen suuhun
- Puraisu ehdolla että tytön jalka on suussa.
Puremisjälkeen johtavat mahdolliset skenaariot näyttävät graafisena mallina tältä:
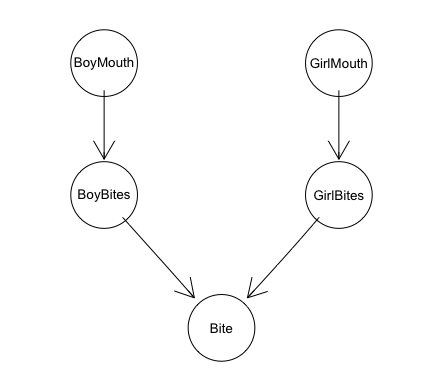
Tästä seikkailu jatkuukin jo kaavojen hahmottelemisella ja isä löytää tilanteeseen sopivia merkintöjä Bayesläisen tilastotieteen pyhästä kirjasta (Gelman ym., Bayesian data analysis 3). Koska kovia todisteita, eli dataa, on niukasti tarjolla, päättelyn täytyy perustua sellaisiin palasiin, joita pystyy prioritiedon perusteella arvioimaan. Lopulta isä päätyy loitsuun, joka kuuluu seuraavasti:
![]()
Tätä kryptistä koodia isä lähtee purkamaan palanen kerrallaan. Yhtäsuuruusmerkin oikealla puolella oleva palanen ![]() on vastaus kysymykseen: ”Kuinka monta kertaa todennäköisempää on että tyttö laittaa jalan oman suuhunsa, kuin että poika laittaa sen?” Tytön on aiemmin isä nähnyt tutkivan varpaitaan lähietäisyydeltä ja fysiologisesti jalan laittaminen suuhun olisi mahdollista. Suuhun asti jalan työntämisestä ei kuitenkaan vielä ole muistijäljissä todisteita. Poika taas on innokkaasti viimeaikoina jaellut pusuja ja suupöristyksiä perheenjäsenilleen milloin minnekin. Lisäksi fysiologisesti toimenpide on pojalle helpompi. Tältä pohjalta isä päätyy arvioon: Todennäköisyys, että tyttö olisi laittanut jalkansa suuhun tässä tilantessa on noin puolet siitä, että poika olisi laittanut siskonsa jalan suuhun.
on vastaus kysymykseen: ”Kuinka monta kertaa todennäköisempää on että tyttö laittaa jalan oman suuhunsa, kuin että poika laittaa sen?” Tytön on aiemmin isä nähnyt tutkivan varpaitaan lähietäisyydeltä ja fysiologisesti jalan laittaminen suuhun olisi mahdollista. Suuhun asti jalan työntämisestä ei kuitenkaan vielä ole muistijäljissä todisteita. Poika taas on innokkaasti viimeaikoina jaellut pusuja ja suupöristyksiä perheenjäsenilleen milloin minnekin. Lisäksi fysiologisesti toimenpide on pojalle helpompi. Tältä pohjalta isä päätyy arvioon: Todennäköisyys, että tyttö olisi laittanut jalkansa suuhun tässä tilantessa on noin puolet siitä, että poika olisi laittanut siskonsa jalan suuhun.
Viimeinen palanen kaavassa, ![]() , on taas vastaus kysymykseen: ”Kuinka paljon (suhteellisesti) suurempi todennäköisyys on tytön puraisulle silloin kun tytön jalka on suussa verrattuna pojan puraisulle vastaavassa tilanteessa.” Sisaruksista vanhempana poika on jo hyvin oppinut hallitsemaan hampaiden käyttöä, eikä pusujen sivutuotteina tulleista puraisuista ole enää vähään aikaan muistikuvia. Kyseessä voi myös olla tahallinen vahingoittaminen, mutta yleensä taistelut leluista ovat johtaneet tönimiseen tai läpsimiseen. Tyttö taas ei ole vielä oppinut kunnolla hallitsemaan tuoretta purukalustoaan ja itse kukin perheenjäsen on viime aikoina joutunut hänen näykkäilyjen kohteeksi. Isä päätyy tässä kohtaa arvioon, että jos jalka on suussa niin tyttö puraisee sitä 2.5 kertaa poikaa todennäköisemmin.
, on taas vastaus kysymykseen: ”Kuinka paljon (suhteellisesti) suurempi todennäköisyys on tytön puraisulle silloin kun tytön jalka on suussa verrattuna pojan puraisulle vastaavassa tilanteessa.” Sisaruksista vanhempana poika on jo hyvin oppinut hallitsemaan hampaiden käyttöä, eikä pusujen sivutuotteina tulleista puraisuista ole enää vähään aikaan muistikuvia. Kyseessä voi myös olla tahallinen vahingoittaminen, mutta yleensä taistelut leluista ovat johtaneet tönimiseen tai läpsimiseen. Tyttö taas ei ole vielä oppinut kunnolla hallitsemaan tuoretta purukalustoaan ja itse kukin perheenjäsen on viime aikoina joutunut hänen näykkäilyjen kohteeksi. Isä päätyy tässä kohtaa arvioon, että jos jalka on suussa niin tyttö puraisee sitä 2.5 kertaa poikaa todennäköisemmin.
Loitsun lopputulosta voidaan siis arvioida numeroarvoilla: 0.5 * 2.5. Tässä kohtaa isä hyödyntää vielä tietoa, ettei muita epäiltyjä ole ja päättää jättää huomiotta epätodennäköisen skenaarion, jossa molemmat olisivat syyllisiä. Loitsu yksinkertaistuu nyt muotoon: ![]() . Vaikka tässä kohtaa isää alkaakin jo uuvuttaman, hän vielä pinnistää pari riviä yhtälön pyörittelyä ja saa lopulta todennäköisyysarviot syyllisyyksille: Tyttö 56%, poika 44%.
. Vaikka tässä kohtaa isää alkaakin jo uuvuttaman, hän vielä pinnistää pari riviä yhtälön pyörittelyä ja saa lopulta todennäköisyysarviot syyllisyyksille: Tyttö 56%, poika 44%.
Isä huokaisee helpoituksesta. Todennäköisin skenaario voisi sittenkin olla, että tyttö on vienyt omien varpaiden tutkimisen hieman normaalia pidemmälle ja ensimmäistä kertaa nyt itse kokenut tuoreen purukalustuksensa tehon. Pojan kiusanteko tai vahinko pusun yhteydessä ovat edelleen varteenotettavia vaihtoehtoja, mutta rankaisu olisi käytettävissä olleiden tiedonmurusten pohjalta ollut paha virhe.
Jälkikirjoitus
Edellisen tarinan isän harjoittama tutkimus on hyvin epätäsmällistä tiedettä, koska kunnon todisteet loistavat poissaolollaan ja prioritiedon pohjalta tehdyt arviot ovat hyvin pitkälti sitä kuuluisaa mutu-tuntumaa. Tämä on kuitenkin hyvä esimerkki arkielämän tilanteessa, jossa data nyt on mitä on, mutta joku päätös on kuitenkin tehtävä. Olennaista silloin on muotoilla tapahtuma sellaiseksi palasiksi, joita pystyy jollain tavoin perustellusti arvioimaan.
Jos tätä todennäköisyyslaskentaan pohjautuvaa päättelyä laajennetaan aikuisten rikosten maailmaan, päästään mielenkiintoisten moraalisten pohdintojen äärelle. Yhtiökumppanini sekä ex-työkaverin kanssa taannoin pohdiskeltiin sopivaa syyllisyyden todennäköisyyttä, josta ylöspäin tuomio pitää langettaa. Olimme yhtä mieltä siitä ettei se voi olla 100%, koska jokainen puolustusasianajaja keksisi aina jonkun teoriassa mahdollisen skenaarion, joka selittäisi päämiehensä syyttömyyden eikä ketään rankaistaisi. Sen sijaan esim. 80% tuntuu aivan liian alhaiselta, jos asiaa ajattelee omalle kohdalle. Ei tunnu oikein reilulta, mikäli joutuisin syyttömänä vankilaan silloin kun ulospäin näkyvät todisteet puhuvat vain 80% todennäköisyyden puolesta. Mutta mikä olisi sitten hyvä raja tällä välillä? Siinäpä pähkinää purtavaksi etsivälle jos toisellekin.
