ennustaminen | Statistition

Archives for : ennustaminen

Analytiikan alalajit

Posted by :Statisticko On : 20.6.2019

Category: Algoritmit, Ennustaminen, Liiketoiminta, Päätöksenteko

Tags:BI, data, ennustaminen, kausaalisuus, liiketoiminta, optimointi, päätöksenteko

Sijoittajamestari Ray Dalio kokosi elämässään oppimansa asiat teokseen Principles ja päätökseen tekoon liittyvä ensimmäinen periaate kuuluu näin:

”Recognize that 1) the biggest threat to good decision making is harmful emotions, and 2) decision making is a two-step process (first learning and then deciding).”
Ray Dalio

Datan analysointi tai datatieteily liityy nimenomaan ympäristöstä oppimiseen ilman tunteiden aiheuttamia vääristäviä tunteita niin että voitaisiin tehdä mahdollisimman valistuneita päätöksiä.

Kun tehdään liiketoimintaa tukevaa analyysiä, datan analysointi jaetaan tyypillisesti neljään alalajiin riippuen, mitä työllä tavoitellaan. Eri konsultit voivat järjestellä ne hieman eri tavoilla, mutta itse mielelläni järjestäen ne seuraavasti analyyttisen haastavuuden mukaan helpoimmasta vaikeimpaan:

Kuvaileva analytiikka (Mitä tapahtui?)
Ennakoiva analytiikka (Mitä tulee tapahtumaan?)
Diagnosoiva analytiikka (Miksi jotain tapahtui?)
Ohjaileva analytiikka (Mitä kannattaisi tehdä?)

Kolme ensimmäistä liittyy oppimiseen ja viimeinen päätöksentekoon opitun pohjalta.

Hukkuvat jäätelönsyöjät

Avataan sitten näitä alalajeja esimerkin avulla. Hukkuvat jäätelönsyöjät on monelle jo liiankin tuttu esimerkki riippuvuussuhteista, mutta ratsastetaan nyt vielä kerran sillä, koska se kaikessa tomppeluudessaan kuitenkin hyvin demonstroi oleellisia pointteja.

Olkoon meillä toimeksiantona jäätelökioskiyrittäjän auttaminen ja myyntiä ilmiönä kuvaa seuraava graafi.

Lämpötilan nousu aiheuttaa enemmän sekä jäätelön myyntiä että hukkumiskuolemia. Hukkumisen ja jäätelön myynnin välillä ei ole syy-seuraus-yhteyttä.

Graafissa olevien syy-seuraus-yhteyksien pohjalta olen nyt simuloinut 300 havaintoa, jonka kanssa seuraavissa esimerkeissä operoidaan.

Kuvaileva analytiikka

Kuvaileva analytiikka vastaa siis kysymykseen ”Mitä tapahtui?”. Vastaus löytyy raporteista, joissa on tilastollisista tunnuslukuja ja graafisia kuvioita. Yritysmaailmassa tätä analytiikan alalajia kutsutaan termillä Business Intelligence (BI). Meidän dataa 300 aiemmasta viikkohavainnosta kuvaavat esim. seuraavat tunnusluvut.

	TEMP (C)	SALES (EUR)	DROWNED
Keskiarvo	19.6	13035	1.15
Keskihajonta	5.34	1315	3.52

Lisäksi mielenkiinnon mukaan tunnuslukuja voisi vertailla eri ryhmien, esim. viikonpäivien tai jäätelömakujen, välillä.

Keski- ja hajontalukujen lisäksi havaintoja voi kuvata muuttujien välisillä korrelaatiokertoimilla ja graafisilla kuvaajilla. Seuraava graafi ei ole välttämättä kauneimmasta päästä, mutta minulle sen piirtäminen on osa perusprosessia uuteen aineistoon tutustuttaessa. Siinä on paljon informaatiota tiiviisti ilmaistuna ja sen saa tulostettua R-ohjelmistolla yhdellä komennolla.

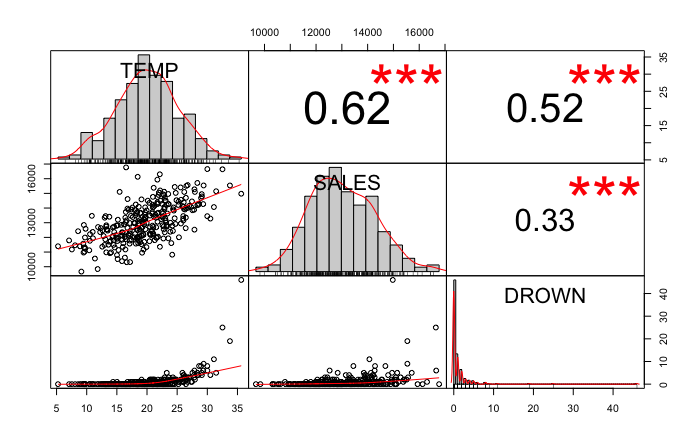
Lävistäjällä ovat jokaisen muuttujan omat jakaumat. Vasemmalla alhaalla ovat parittaiset sirontakuviot. Oikella ylhäällä ovat parittaiset korrelaatiokertoimet ja niiden merkitsevyystasot tähtinä.

Kuvaajasta nähdään mm. seuraavaa:

Lämpötilan ja myynnin havainnot ovat jakautuneet symmetrisesti keskiarvon ympärille ja muistuttaa normaalijakaumaa. Hukkumisten lukumäärän jakauma on vino.
Kaikkien muuttujien väliset korrelaatiokertoimet (luvut oikealla ylhäällä) ovat positiivisia, joten muuttujilla on ollut taipumus saada isoja arvoja yhtäaikaa.
Kaikki muuttujien väliset korrelaatiokertoimet ovat tilastollisesti erittäin merkitseviä (punaiset tähdet), joten ei ole uskottavaa että korrelaatiokertoimet poikkeavat nollasta vain sattumalta.
Suora viiva kuvaa hyvin myynnin ja lämpötilan välistä yhteyttä. Hukkumisen ja muiden muuttujien välisen yhteyden kuvaamiseen suora viiva ei ole paras mahdollinen (kuviot vasemmalla alhaalla).

Kuvaileva analytiikka keskittyy kuvailemaan historian tapahtumia, mutta vastuu siitä, mitä tulee tapahtumaan tulevaisuudessa jää täysin raportin lukijalle.

Ennakoiva analytiikka

Vaikka historiakin on mielenkiintoista, vielä kiinnostavampaa liiketoiminnan kannalta on se mitä on odotettavissa tulevaisuudessa. Mennyt ei ole tae tulevasta, mutta historiaan perustuen voi tehdä valistuneita arvioita eri tulevaisuuden skenaarioiden todennäköisyyksistä.

Esimerkissämme mielenkiinnon kohteena on ennustaa tulevan viikon jäätelön myyntimäärä. Pelkään BI-raporttiin (kuvaileva analytiikka) perustuen paras arvaus olisi historiallinen keskiarvo 13035 euroa. Simuloin tässä 100 uutta havaintoa tulevista viikoista ja historialliseen keskiarvoon perustuva arvaus ei ole hassumpi: keskimäärin ennuste on 7.3% pielessä.

Olisimme voineet kuitenkin ottaa askel eteenpäin ennakoivan analytiikan puolelle ja muodostaa regressiomalli, jossa hyödynnetään tietoa päivän lämpötilasta. Lämpötilan ja myynnin välinen korrelaatiokerroinhan oli varsin suuri, 0.62. Tällaisen mallin tarjoama paras arvaus seuraavan viikon myynnistä menee nyt uusilla havainnoilla keskimäärin 6.5% pieleen.

Vaikka hukkumisilla ei ole syy-seuraus-suhdetta myyntiin, ei sen hyödyntämiselle ennustamisessa ole estettä. Jos sen lisää toiseksi selittäjäksi samaan regressiomalliin lämpötilan kanssa ei siitä iloa kuitenkaan ole, koska lämpötila jo yksinään selittää hukkumisten ja myynnin välisen yhteyden. Mutta mikäli vahingossa olisimme hukanneet historian lämpötilahavainnot, olisi hukkumiskuolemat hyvä apumuuttuja. Pelkästään edellisen viikon hukkumisiin perustuvat ennusteet ovat tässä tapauksessa 6.7% pielessä. Lopuksi vielä yhteenveto, kuinka tarkasti saatiin 100 uutta myyntihavaintoa ennustetttua.

Ennustaja	Keskimääräinen virhe
Oma historia	7.33%
Lämpötila	6.45%
Hukkumiset	6.73%
Lämpötila+Hukkumiset	6.43%

Regressiomallien lisäksi muita ennustamisen työkaluja ovat aikasarja-analyysi silloin kun kiinnitetään erityistä huomiota ajassa systemaattisesti toistuviin kuvioihin. Sitten kun käsillä on ajassa stabiili ilmiö, mutta paljon potentiaalisia selittäjiä sekä paljon dataa, arvoon arvaamattomaan nousevat erilaiset koneoppimisalgoritmit kuten neuroverkot tai päätöspuut. Mikäli useiden potentiaalisten selittäjien lisäksi meillä on hieman ymmärrystä näiden selittäjien keskinäisistä riippuuvuussuhteista, voidaan dataa ja asiantuntemusta yhdistää Bayes-verkkojen avulla tai simuloimalla maailman menoa ymmärryksemme rajoissa.

Käyttipä mitä tahansa näistä ennustusmenetelmistä tai jotain niiden yhdistelmää, meillä on kaksi ikävää kiusaa:

Ylisovittaminen: tietämättämme yritämme tulevaisuutta ennustaa sellaisilla historiallisilla piirteillä, jotka ovat toteutuneet aiemmin vain sattumalta eivätkä kuvaa ilmiötä tulevaisuudessa. Tätä ongelmaa olen ruotinut aiemmin tässä kirjoituksessa.
Pysyvät muutokset muuttujissa, joita ei olla aiemmin mitattu. Esimerkiksi lakimuutokset voivat ohjata ihmisiä käyttäytymään tulevaisuudessa eri tavalla kuin mihin aiemmin olemme tottuneet. Tätä ongelmaa olen käsitellyt tarkemmin tässä kirjoituksessa.

Kiitos mm. edellä mainittujen haasteiden ennakoivassa analytiikassa vaaditaan jo huomattavasti korkeamman tason koulutusta kuin kuvailevassa analytiikassa.

Diagnosoiva analytiikka

Diagnosoivalla analytiikalla pyritään löytämään asioiden välisiä syy-seuraus-yhteyksiä. Tieteellisen uteliaisuuden lisäksi liiketoiminnan kannalta kiinnostavaa voisi olla selvittää, mitä asioita muuttamalla saisimme myyntiä kasvatettua. Ennakoivan analytiikan maailmassa korrelaatiokertoimet antoivat hyviä vinkkejä, mitä muuttujia voisimme hyödyntää ennustamisessa. Kun tavoitteena on puuttua itse peliin asioiden muuttamiseksi, vain korrelaatioita tuijottamalla voisimme päätyä raportoimaan jäätelöyrittäjälle: ”Myynnin edistämiseksi kannattaa alkaa hukuttamaan ihmisiä”. Tämähän ei alkuunkaan pidä paikkansa niinkuin kohta tullaan näkemään.

Varmin tapa syy-seuraus eli kausaaliyhteyden selvittämiseksi on tehdä satunnaisettu koe riittävällä määrällä toistoja. Näistä klassinen esimerkki on antaa satunnaisesti toisille koehenkilöille oikeaa lääkettä ja toisille koehenkilöille lumelääkettä. Vaikutuksia vertailemalla voidaan saada selville, onko lääkkeessä oikeasti tehoa. Modernimpi esimerkki on verkkokaupan käyttöliittymän A/B-testaus, jossa satunnaisesti toisille asiakkaille nettisivulle näytetään punainen nappi ja toisille sininen nappi ja vertaillaan vaikuttaako napin väri sen klikkausten määrään.

Mikäli satunnaistetut kokeet eivät ole mahdollisia, voidaan yrittää metsästää luonnollisia kokeita. Esimerkiksi voidaan ottaa seurantaan henkilöt, jotka ovat juuri ja juuri päässeet läpi lääkiksen pääsykokeista ja vertailla tätä joukkoa niihin jotka jäivät niukasti ulos lääkiksestä. Voidaan olettaa että pienet erot pääsykokeen pistemäärissä jouhtuvat suurelta osin satunnaistekijöistä ja näin ollen on luotettavaa tehdä päätelmiä lääkiksen kausaalivaikutuksista loppuelämän onnellisuuteen.

Viimeisimpien vuosikymmenien aikana on erityisesti Judea Pearlin johdolla kehitetty kausaalimalleja, jotka auttavat tekemään kausaalipäätelmiä myös silloin kun käytössä havaittua dataa, mutta ei voida tehdä satunnaistettuja kokeita. Niissä aluksi pitää pystyä aiempiin tutkimuksiin perustuen rakentamaan graafi, josta näkee mitkä muuttujat vaikuttavat mielenkiinnon kohteina oleviin muuttujiin. Mikäli tärkeimmät näistä taustamuuttujista on mitattu, kausaalipäätelmät voivat olla mahdollisia.

Meidän kolmen muutttujan tapauksessa ilmiötä kuvaava graafi on esitelty kirjoituksen alussa. Tässä hyvin yksinkertaisessa maailmassa pystymme tutkimaan hukkumisten kausaalityhteyttä myyntiin. Kun laitamme sekä lämpötilan, että hukkumiset samaan regressiomalliin selittämään myyntiä, hukkumisella ei ole mitään selitysvoimaa, koska lämpötila on kaiken juurisyy. Näin ollen data näyttää, että ihmisiä on aivan turha alkaa hukuttamaan myynnin edistämiseksi.

Monimutkaisempien ilmiöiden tutkiminen kausaalimalleihin tukeutuen on itselläni vielä vaiheessa, joten ei kannata puhua tässä siitä sen enempää. Silti osa omaa analyysiprosessia on hahmotella graafiksi erilaisia potentiaalisia taustalla lymyileviä syy-seuraus-yhteyksiä, joita voi sitten asiaan paremmin vihkiytyneet haastaa. Mikäli mielenkiinto kausaalimalleihin heräsi, kannattaa aloittaa Judea Pearlin tietokirjasta ”The book of why”, josta Kimmo Pietiläinen on tehnyt myös suomenkielisen käännöksen: ”Miksi – syyn ja seurauksen uusi tiede”.

Ohjaileva analytiikka

Ohjaileva analytiikka on tässä lajittelussa laitettu viimeiseksi, koska pohjalla pitää olla alemman tason analytiikkaa päätöksenteon tueksi. Täältä huipulta kannattaa kuitenkin aina aloittaa pohtimalla, mitä halutaan tehdä. Mihin liittyviä päätöksiä analytiikalla halutaan parantaa? Esimerkkejä:

Halutaan kehittää jäätelönmyynnin logistiikkaa: miten paljon mitäkin makua pitäisi toimittaa kioskille, että asiakkaat saavat mitä haluavat, mutta jäätelöä ei tarvitsisi kohtuuttomia määriä pakastimessa varastoida. – > Ratkaisu: Päätöksenteon tueksi tarvitsemme ennakoivaa analytiikkaa, jolla arvioidaan kuinka paljon mitäkin makua menee ensi viikolla.
Halutaan lisätä jäätelön kysyntää. -> Ratkaisu: Diagnosoiva analytiikka. Johtopäätös on se, että korkeammat lämpötilat johtaisivat korkeampaan myyntiin. Mutta koska kaikki säiden hallitsemiseen kykenevät tahot ovat niin kallispalkkaisia, ei tällaista hanketta kannata toteuttaa. Laitetaan resurssit muun toiminnan kehittämiseen.

Kun pohjalla on riittävästi oppia analytiikan alemmilta tasoilta, ohjaileva analytiikka on pääasiassa erilaisia optimointialgoritmeja. Lisäksi on olemassa itseoppivia päätöksentekoalgoritmeja, jotka päivittävät omaa ymmärrystä aina päätöksestä tulleen palautteen perusteella.

Päätöksenteon optimointi on liian laaja aihe alkaa tässä syvemmin käsiteltäväksi, mutta se vaanii kaiken liiketoiminta-analytiikan taustalla. Ennen hosumista liian pitkälle datan kanssa, olisi hyvä ymmärtää mitä päätöksiä halutaan parantaa. Se mahdollistaa, että analytiikan alimmalta portaalta ponnistaessa edetään oikeaan suuntaan. Toisinaan matkalla opitaan jotain uutta, jonka vuoksi kurssia joudutaan kääntämään. Tämä tekee seikkailusta kuin seikkailusta entistä jännempää.

Lopputurinat

Dataan pohjautuvalla analytiikalla on useita eri tasoja ja niiden sisällä eri etenemispolkuja. Jotta varmistetaan datan penkomisen hyödyllisyys, aluksi pitäisi kirkastaa, mitkä päätöksentekoprosessit yrityksessä kaipaavat hiomista. Sitten valitaan sellainen polku, jota olemassa olevan datan pohjalta on mahdollista edetä. Lopulta päätöksenteko on kaksivaiheista: ensin opitaan, sitten päätetään.

Mihin voi luottaa informaatioähkyn keskellä?

Posted by :Statisticko On : 29.9.2017

Category: Ennustaminen, Epävarmuus, Osakesijoittaminen, Tutkimukset, Vedonlyönti, Yhteiskunta

Tags:asiantuntijat, ennustaminen, infomaatio, tiede, uutiset, vedonlyönti

Internet on tiedon valtatie. Mutta valitettavasti se on myös temmellyspaikka monenkirjavien totuutena myytävien uskomusten levittäjille.

Tim Ferriss kirjoitti kirjassaan ”The 4-Hour Workweek”, kuinka yksi keino hankkia lisätuloja on alkaa asiantuntijaksi. Ferrissin mukaan 4 viikkoa riittää asiantuntijastatuksen haalimiseen uudella alalla. Tosin ei niin hyvän, että saisi kunnioitusta kyseisen alan oikeilta asiantuntijoilta, mutta sellaisen uskottavuuden että voi muodostaa riittävän suuren asiakaskunnan ihmisistä, jotka eivät tunne alaa.

Omalta erikoisalaltaan osaa erottaa juttujen sisällön perusteella nämä puoskarit tohtoreista, mutta entä kun puhe on aiheesta, josta itsellä ei ole kummoisia taustatietoja? Mihin tietoon tässä maailmassa voi luottaa?

Tieteellinen prosessi

Tiedon etsimisessä ei voi täysin nojautua yksittäiseen tutkimukseen. Yksittäisen tutkimuksen lopputulos voi osua harhaan monestakin syystä ja useamman vuoden vanha tutkimus on voitu jo kumota uusimmissa tutkimuksissa. Sen sijaan julkaisujen sarjasta koostuva tieteellinen prosessi johtaa pikkuhiljaa aina vaan lähemmäksi totuutta. Tieteellisen prosessiin kuuluu, että koko ajan mennään eteenpäin ja pyritään etsimään virheitä vanhoista omista olettamuksista. Hyvä tapa aloittaa uuteen aiheeseen tutustuminen on etsiä viimeisin review-artikkeli, joka kokoaa yhteen, mitä tähän mennessä eri tutkijat ovat löytäneet.

Uutisointi

Monessa muussa asiassa niin hyvin toimiva markkinatalous tuntuu yskivän tiedon levityksessä. Yliampuvat shokkiuutiset ja liian yksinkertaiset ratkaisut monimutkaisiin ongelmiin myyvät paremmin kuin analyyttinen asioiden punnitseminen eri näkökulmista. (Ketosen ja Myllyrinteen tiivistys). Tämä siitä huolimatta, että perusteellisesti analysoidun tiedon tehokkaampi leviäminen auttaisi meitä kaikkia tekemään parempia päätöksiä, joilla voisi nostaa itsemme ja läheistemme terveydellistä + taloudellista hyvinvointia.

Päivittäisen uutisvirran seuraaminen voi olla jopa haitallista asioiden ymmärtämisen kannalta, mitä tässä kirjoituksessa hyvin perustellaan. Itse pyrin seuraaman maailman menoa hieman suodatettuna niin että luen uutisen netistä vasta kun joku analyyttisena pitämäni Twitter-seurattava kommentoi uutista mielenkiintoisena.

Twitterissä olen kokenut hyödylliseksi seurattavaksi myös vahvan tieteellisen taustan omaavat aktiiviset ”bull shit detectorit” (esim. Markku Niemivirta @mniemivirta) ja harhaanjohtavalta otsikoinnilta suojelijat (esim. @klikinsaastaja). Nämä säästävät omaa aikaani harhaanjohtavien uutisten lukemiselta.

Tieteellistä lähestymistapaa uutisten käsittelyyn edustaa nettisivusto Rootclaim. Kun maailmalla on tapahtunut jotain, jossa totuutta on vaikea hahmottaa kaikkien asian ympärillä pyörivien huhujen joukosta, Rootclaim ottaa asian punnittavaksi. Jäsenet muodostavat kilpailevia hypoteeseja vaihtoehtoisista totuuksista ja kokoavat yhteen tiedonmurusia asian ympärillä eri lähteistä. Lopputuloksena on Bayesläisen päättelyn tuloksena todennäköisyydet eri hypoteesien todennäköisyyksille. Kuka tahansa voi osallistua prosessiin tiedottamalla uusista tiedonjyväsistä ja todennäköisyydet sitä mukaa päivittyvät. Tällä hetkellä sivustolla punnitaan ainakin Malesialaisen lentokoneen katoamista, rokotteiden sivuvaikutuksia ja Syyriassa tapahtunutta kemiallista asehyökkäystä.

Vedonlyönti

”Put your money where your mouth is or shut up.”

Ne ketkä oikeasti ymmärtävät asioista, voivat myös lyödä vetoa näkemystensä puolesta. Silloin kun vedonlyönti on mahdollista, erinomainen näyttö ymmärtämisestä on voitollisen vedonlyöntihistorian esittely. Tosin tässä kirjoituksessani kävi ilmi että vetoja pitää löytyä aika paljon historiasta, että sillä voisi tilastollisesti osaamisensa todistaa. Kuitenkin jos on edes valmis laittamaan rahaa likoon näkemyksensä puolesta pelkän leukojen loksuttamisen sijaan, on se jo merkki uskottavuuden suuntaan.

Vedonlyöntikulttuuri kukoistaa penkkiurheilijoiden keskuudessa ja talousasioissa voi ottaa näkemystä joko osake- tai johdannaismarkkinoilla. Vedonlyöntifirmat ottavat myös kiitettävästi vetoja vastaan poliittisista vaaleista. Kaipaisin kuitenkin lisää herrasmiesvedonlyöntikulttuuria muillekin elämän osa-alueille. Silloin erimieltä olevien ei tarvitsisi loputtomasti jankuttaa SoMessa vaan sopia aiheeseen liittyvä veto ja jatkaa elämää. Vetojen lopputulokset kun vielä päivittyisivät julkiselle sivustolle niin pikkuhiljaa vetojen kertyessä alkaisi hahmottumaan, kuka on vahvemmin ja kuka heikommin asian ytimessä.

Asiantuntijoiden nahka

Kun ottaa neuvoja vastaan asiantuntijalta tai sellaisena esiintyvältä, pitää aluksi varmistaa missä pelissä tällä henkilö on niin sanotusti oma nahka pelissä (”skin on the game”). Varsinkin jos henkilö saa kaikki tulonsa yhdestä lähteestä, ensisijainen peli hänellä on työpaikkansa ja asemansa säilyttäminen. Esim. apteekkarilta voi saada hyvän näkemyksen siihen, mitä lääkkeitä eniten myydään. Sitten kun pohdinnan alla on apteekkimonopolin hyödyllisyys yhteiskunnalle, voi näkemys olla vähän yksipuolinen. Eikä kannata odottaa, että rivityöntekijätkään purevat ainoaa ruokkivaa kättä.

Asiantuntijalta kannattaa myös muotoilla kysymykset sellaiseen muotoon, missä vahvasti tuodaan hänen omaa nahkaansa peliin. Esim. kilpailevista hoitomuodoista voi kysyä lääkäriltä muodossa: ”Millä menetelmällä hoitaisit tällaisessa tapauksessa itseäsi / lastasi?”

Superennustajien ominaisuudet

Philip E. Tetlockin ja Dan Gardnerin kirjoittamassa ja Terra Cognitan suomentamassa kirjassa Superennustajat kerrotaan ”Good Judgment” – tutkimusprojektista, jossa lukuisat tavalliset ihmiset tekivät ennusteita mitä erilaisista tulevaisuuden tapahtumista, kuten poliittisten konfliktien tai taloudellisten tunnuslukujen kehittymisestä. Hieman yllättävä tulos oli, että tietyt samat henkilöt vuodesta ja aiheesta toiseen erottuivat muista edukseen. Kirjoittajien mukaan vieläpä paljon paremmin kuin mitä pelkkä sattuma antaisi odottaa. Näitä tutkimuksen kestomenestyjiä kirjoittajat kutsuvat superennustajiksi. Ammatillisen taustan suhteen superennustajilla ei ollut mitään yhteistä selittäjää, mutta seuraavia yhteisiä taipumuksia heistä löytyi maailmankatsomuksen, kykyjen ja ajattelutapojen suhteen:

Varovainen (mikään ei ole varmaa)
Nöyrä (todellisuus on äärettömän monimutkainen)
Epädeterministinen (tapahtuva ei ole ennalta määrätty, eikä sen tarvitse tapahtua)
Aktiivisesti mieleltään avoin (uskomukset ovat testattavia hypoteeseja, eivät suojattavia aarteita)
Älykäs ja tietävä jolla on ”tunnustuksen” saamisen tarve (älyllisesti uteliaita, ongelmista ja mentaalisista haasteista nauttivia)
Reflektiivinen (itsetutkiskeleva ja itsekriittinen)
Numerotaitoinen (sinut numeroiden kanssa)

Lisäksi kirjassa mainitaan, että superennustajat pyrkivät jatkuvasti päivittämään ja parantamaan omia arvioitaan. Ohjelmointikielellä he ovat ikuisia ”beta-versioita” itsestään. Voitaneen lisätä, että he ovat käveleviä tieteellisiä prosesseja.

Mikäli kokee vedonlyönnin liian uhkapelinä, voi asiantuntijuuttaan osoittaa pitämällä julkisesti kirjaa ennusteistaan. Good Judgment – projektilla on avoin yhteisö, johon kuka tahansa voi liittyä ja alkaa tekemään ennusteita haluamistaan aiheista. Koska kirjanpidon hoitaa yhteisön verkkosivut automaattisesti, ei jälkikäteen voi pieleen menneitä ennustuksia piilotella. Tämän blogikirjoitukseni innoittamana itsekin kävin nyt kirjautumassa mukaan yhteisöön nimimerkillä ”Riski-Risto”.

Esimerkki

Lopuksi nostan esimerkkinä esiin yhden henkilön, jota en tunne henkilökohtaisesti millään tavalla, mutta hän on onnistunut herättämään valtavaa kunnioitusta. Kyseessä on osakerahaston hoitajana työskentelevä Anders Oldenburg. Vaikka lähtökohtaisesti välttelen aktiivisen salkunhoidon kuluja, tässä kohtaa olen tehnyt poikkeuksen ja sijoittanut rahastoon.

Tuottohistoria

Andersin hoitama Phoebus – rahasto on ollut pystyssä 15 vuotta yhden ja saman henkilön hoidossa. Tänä aikana rahasto on keskimäärin tuottanut sijoittajille 11.3% vuodessa. Tästä on vähennetty rahaston kulut (TKA) mitkä ovat olleet keskimäärin 1.2% vuodessa. Vertailuindeksin tuottaessa samana aikana 9.5%, saadaan tulokseksi, että Anders on osakevalinnoillaan pystynyt tuottamaan noin 3 % – yksikön verran vuosittaista ylituottoa, josta asiakkaalle on jäänyt hyötynä 1.8 % -yksikköä. Luvut voi käydä tarkemmin läpi täällä.

En ole tarkemmin tutkinut, missä ajassa osakemarkkinoilla erottuvat starat hyvätuurisista keskivertosijoittajasta tilastollisesti. Kutina on että 15 vuotta olisi jonkinlainen, muttei yksinään täysin vakuuttava näyttö.

Skin in the game

Anders on (ainakin omien sanojensa mukaan) sijoittanut itse merkittävän osan varallisuudestaan omaan Phoebus – rahastoonsa ja on rahaston suurin yksittäinen sijoittaja. Tämän luulisi takaavan, että rahastossa on Andersilla itsellään oma nahka mukana samassa pelissä kuin muilla sijoittajilla.

Superennustajan ominaisuudet

Oleellinen osa luottamuksen kehittymistä on ollut Andersin pitämä Phoebus – blogi, jossa hän kommentoi yhtiövalintojaan ja maailmaa niiden ympärillä. Mitä tulee Tetlockin ja Gardnerin mainitsemiin superennustajien ominaisuuksiin, Anders suorastaan korostaa epävarmuutta aina liikkuessaan kirjoituksissaan alueella, jota ei ole perinpohjin tutkinut. Hän myös paljon korostaa satunnaisuutta yritysten lyhyen ajan voitoissa. Lisäksi hän käy avoimesti läpi huonojakin osakevalintoja menneisyydestä ja pyrkii oppimaan virheistään.

Näihin ominaisuuksiin nojautuen olen uskaltanut antaa keskimääristä 1.2% vuosittaisista kuluista huolimatta palan sijoitusomaisuuttani Andersin käsiin ja sen lisäksi pyrin imemään hänen blogista vaikutteita maailman tutkimiseen analyyttisesti. Tämä siitä huolimatta, etten omista minkäänlaista sosiaalista suhdetta kyseiseen kaveriin tai hänen edustamaansa yritykseen.

Tiivistelmä

Ominaisuudet, jotka nostavat asiantuntijan uskottavuutta:

Taustalla pitkä tieteellinen prosessi
Julkinen vedonlyönti, sijoitus tai ennustus -historia
”Skin in the game” samassa pelissä tiedon objektiivisuuden kanssa
Nöyrän analyyttiset ”superennustajan” ominaisuudet

Ylisovittaminen, case jalkapallojoukkueiden budjetit

Posted by :Statisticko On : 31.10.2016

Category: Ennustaminen, Epävarmuus, Urheilu, Yleinen

Tags:ennustaminen, informaatiokriteeri, pelaajabudjetti, RMSE, selitysaste, valioliiga, ylisovittaminen

Kun numeroaineiston perusteella tehdään tutkimusta, helppo vaihe on oppia ymmärtämään, minkälainen ilmiö on ollut kyseisessä aineistossa. Usein varsinainen mielenkiinnon kohde kuitenkin ymmärtää, mitä voisi tapahtua samassa ilmiössä aineiston ulkopuolella ja ehkä jopa ennustaa tulevaisuutta. Tässä vaiheessa on helppo langeta syntiin nimeltä ”ylisovittaminen”.

Valioliigaseurojen pelaajabudjetit

Tutkitaan edellistä Englannin Valioliigan jalkapallokautta 2015/2016. Meitä kiinnostaa, kuinka joukkueen pelaajabudjetti selittää joukkueen saavuttamaa pistemäärää sarjataulukossa. Tässä minitutkimuksessa olemme päätyneet tilanteeseen, jossa meillä on käytettävissä budjettitiedot ja sarjapisteet vain kymmeneltä satunnaiselta joukkueelta. Aineisto (lähde) näyttää seuraavalta:

Vaikuttaisi, että rahalla on odotettua vaikutusta, eli pisteet keskimäärin kasvavat kun budjettikin kasvaa. Mutta minkä muotoinen ”kasvukäyrä” on? Vaikka mahdollisesti muitakin hyviä malleja voisi löytyä, pysytään yksinkertaisuuden vuoksi polynomifunktioissa ja esitellään niistä ensin kaksi tapausta.

Ensimmäinen ajatus voisi olla kokeilla ensimmäisen asteen funktiota, mikä on tilastotieteen / ekonometrian peruskurssilta tuttu lineaarinen regressiomalli: $Points = a + b \cdot Salary$ .

Ajatuksena, on että pistemäärä kasvaa keskimäärin tasaisesti sitä mukaa kun budjettikin kasvaa. Kuvaan olikin jo piirretty sellainen regressiosuora.

Huomattavaa on, että jotkut pisteet jäävät hyvinkin kauaksi suorasta. Me kuitenkin tiedetään, että osumatarkkuutta voidaan kasvattaa kun lisätään selittäjiä, tässä tapauksessa budjetin korkeampia potensseja, malliin. Mikäli työvuorossa sattuu olemaan täydellisyyteen pyrkivä insinööri, hän saattaisi innostua käyttämään hyvinkin korkean asteen, sanotaan vaikka viidennen asteen, polynomia, $Points = a + b_1 \cdot Salary + b_2 \cdot Salary ^2 + b_3 \cdot Salary ^3 + b_4\cdot Salary ^4 + b_5 \cdot Salary ^5$ .

Tällaisen mallin käyrä kulkee paljon paremmin eri havaintopisteiden kautta, minkä voi havaita alla olevasta kuvaajasta.

Selitysasteet

Tilastollisen mallin osumatarkkuutta kyseisessä aineistossa mittaa ns. selitysaste ja alla olevassa taulukossa on ratkaistu mallit 1-5 asteisille polynomifunktioille ja laskettu niiden selitysasteet.

Polynomifunktion aste	Mallin selitysaste (isompi parempi, max 100%)
1. aste (lineaarinen)	20%
2. aste (paraabeli)	22%
3. aste	25%
4. aste	59%
5. aste	59%

Selitysasteen perusteella paras (suurin arvo) malli olisi 5. asteen malli ja se vielä paranisi, mikäli kuudes tai seitsemäs termi lisättäisiin. Maalaisjärkikin kuitenkin alkaa jo kolkutella, että näinköhän kyseinen poukkoilevasti kiemurteleva käyrä kuvaisi ilmiötä oikeasti. Ensimmäinen korkea nyppylä n. 50 miljoonan punnan kohdalla selittyy varmaankin vain sillä, että kyseisellä kaudella poikkeuksellisen hyvin pienellä budjetilla menestynyt Leicester sattui omaaman sen suuruusluokan budjetin. Tuskin on mitään syytä, miksi jatkossa havainnot noudattelisivat juuri tuolla tavalla poukkoilevaa käyrää.

Havaitun aineiston ulkopuolelle

Kun halutaan tietää, kuinka hyvin joku tilastollinen malli toimisi aineiston ulkopuolella, niin selitysasteen sijaan mittarina pitää käyttää informaatiokriteerejä. Tunnetun tällainen on Akaiken informaatiokriteeri, AIC. AIC pyrkii arvioimaan sitä, kuinka hyvin mallimme toimii aineiston ulkopuolella. Se palkitsee kyllä hyvästä selitysasteesta, mutta rankaisee mallissa käytettävien tuntemattomien tekijöiden (tässä tapauksessa b-kertoimet) lukumäärästä ajatuksella ”Yksinkertaisella mallilla on pienempi riski ylisovittamiselle”. Ylisovittamisella tarkoitetaan, sitä että yritetään löytää matemaattinen selitys havaintoaineiston satunnaisvaihtelulle, mikä ei toistu samalla logiikalla aineiston ulkopuolella. Viidennen asteen polynomifunktion on malliesimerkki ylisovittamisesta. Seuraavassa taulukossa on laskettu kaikille viidelle mallillemme AIC:

Polynomifunktion aste	AIC (pienempi parempi)
1. aste (lineaarinen)	82.6
2. aste (paraabeli)	84.4
3. aste	86.0
4. aste	82.0
5. aste	84.0

Koska AIC:ssä pyritään mahdollisimman pieneen lukuun, suositeltu malli on 4. asteen funktio ja heti alkuun kokeiltu lineaarinen 1. asteen funktio jää niukasti hopealle.

(Sivuhuomautuksena kerrottakoon, että AIC :n käyttöön liittyy tiettyjä oletuksia ja sen toiminta on epävarmaa silloin kuin oletukset eivät ole voimassa. Mikäli käyttäisimme Bayesläisiä analyysimenetelmiä, työkalupakista löytyisi esim. WAIC (widely applicaple information criterion), joka toimii yleisemmin.)

Havaittu ennustustarkkuus

Katsotaan vielä lopuksi kuinka sitten ennustamisessa kävikään. Alla olevassa kuvaajassa on alkuperäisten havaintojen päälle sovitettu AIC :n suosittelemat 4. asteen käyrä sekä lineaarinen suora ja lisäksi punaisella värillä loput kymmenen joukkuetta viime kaudelta, mitkä eivät vielä olleet mukana tilastollisessa mallinnuksessa.

Lasketaan, mikä polynomifunktioistamme olisi parhaiten ennustanut näitä punaisia uusia havaintoja. Mittarina käytetään keskineliövirhemittaria, RMSE, mikä on sitä parempi, mitä pienempi.

Polynomifunktion aste	RMSE (pienempi parempi)
1. aste (lineaarinen)	66.7
2. aste (paraabeli)	65.8
3. aste	62.2
4. aste	98.2
5. aste	79.1

Huomaamme, että yksinkertaiset 1.-3. asteen funktiot ennustivat paremmin kuin monimutkaiset 4.-5. asteen funktiot, koska niillä on selvästi pienemmät RMSE-luvut. Ennustuskisan voiton vie lopulta kolmannen asteen funktio.

Ilmiön kuvaaminen

Ne ketkä ovat selvinneet tänne asti, saattavat olla kiinnostuneita siitä, mikä pelaajabudjetin vaikutus nyt olikaan menestykseen. Tässä kirjoituksessa päähuomio on uusien havaintojen ennustamisessa, jolloin ilmiön järjellinen selittäminen ei ole välttämättä edes mielenkiintoista. Nyt kun tuli kuitenkin aloitettua, niin…

Edellä esiteltyjen tunnuslukujen perusteella ei ole tällä pienellä aineistolla selvää, mitä mallia kannattaisi käyttää ilmiön selittämiseen. ”Keep it simple, stupid” -periaatteella vaaka kuitenkin kallistuu tasaisessa tilanteessa yksinkertaisempaan suuntaan. Niinpä sovitetaan lineaarinen regressiomalli nyt koko aineistolle ja se sanoo, että 25 miljoonan punnan budjetin jälkeen yhden miljoonan kasvatus pelaajabudjetissa lisäsi keskimärin 0.11 pistettä sarjan aikana. Toisin sanoen yksi lisäsarjapiste maksoi n. 9 miljoonaa puntaa.

Kuten nyt kaikki tiedämme, esim. Leicester ei paljoa lineaarista mallia kunnioittanut vaan paineli mestaruuteen häntäpään budjetilla. Ei lähdetä kuitenkaan ylisovittamaan mitään maagista 48 miljoonan euron optimibudjettia, vaikka selitysaste mittarina sitä tarjoaisikin.

Statistickon steesit

Kun tilastollisen mallinnuksen tarkoitus on ennustaa uusia havaintoja, on varottava datan satunnaisten piirteiden selittämistä, eli ylisovittamista.
Selitysaste kertoo, kuinka hyvin tilastomalli selittää jo havaittua dataa ja paranee aina kun malliin lisätään selittäviä muuttujia.
Informaatiokriteerit ennustavat mallin toimivuutta havaitun datan ulkopuolella.
Ennustemallin toimintaa kannattaa testata uudella ”testidatalla” aina ennen kuin alkaa tehdä sen avulla suuria päätöksiä.
Ennustemallien rakentaminen on yhdistelmä tiedettä ja taidetta.

Lähdeteoksena useassa kohtaa on käytetty kirjaa Richard McElreath: Statistical Rethinking

Valikoitumisharha ennustuksissa

Posted by :Statisticko On : 31.8.2015

Category: Ennustaminen

Tags:ennustaminen, koripallo, rahastot, unet, valikoitumisharha

Oletko joskus havahtunut siihen, että huomaat nähneesi unessa juuri tapahtuneen asian? Tai onko isoäitisi kertonut ennustaneensa unessa useita merkittäviä tapahtumia elämässään? Mitä tällaisista ennustuskyvyistä pitäisi ajatella? Oma ensimmäinen arvaukseni on että hän on oikeassa. Aivan yhtä oikeassa kuin mustekala Paul ja pankin rahaston markkinointiesite.

Mustekalat urheilutietäjinä

Mustekala Paul tuli tunnetuksi ennustettuaan oikein kaikki 7 Saksan ottelua jalkapallon MM-kisoissa 2010. Paul on valitettavasti nyt jättänyt jo taakseen ennustamisen kuten kaikki muutkin maalliset harrastukset, joten mistähän tällaisia mustekaloja voisi löytää vaikka pian alkaviin koripallon EM-kisoihin? Yksinkertaistetaan hieman tavoitteita ja lähdetään etsimään mustekalaa, joka osaa ennustaa oikein seitsemän ottelua, missä kaikissa on vastakkain tasavahvat joukkueet eikä tasapeli ole mahdollinen lopputulos. Riittää että hankitaan akvaarioon 290 mustekalaa ennustelemaan, niin on 90% todennäköisyys että vähintään yksi heistä ennustaa kaikki oikein. Tosin etukäteen emme tiedä kuka tästä mustekalajengistä se sankari tulee olemaan, mutta eipä se estä hehkuttamasta parasta lonkeroprofeettaa jälkikäteen.

Sosiaalisen median ennustajaguruksi

Toisaalta jos itse haluat olla Paulin kaltainen ennustaja niin sekin onnistuu ja vielä 100% varmuudella. Avaat vaan 128 Twitter-tiliä. Puolella tileistä ennustat ennen ensimmäistä peliä toista joukkuetta ja puolella tileistä toista. Ottelun jälkeen suljet ne 64 tiliä, jotka eivät osuneet oikein. Jäljelle jääneillä 64:llä tilillä ennustat seuraavan koripallopelin voittajaksi molempia joukkueita 32 kertaa. Jatkat tätä samaa rataa, kunnes seitsemän pelin jälkeen sinulla on jäljellä yksi Twitter-tili, jonka aikaleimat todistaa ennustaneesi kaikki 7 peliä oikein etukäteen ja voit alkaa hankkimaan seuraajia. En ole ihan varma tekeekö tämmöinen temppu ketään kulttiguruksi, mutta hahmottaa hyvin valikoitumisharha(utukse)n ideaa.

Valikoidut rahastot

Mikäli käyt pankissa keskustelemassa sijoitusasioista, niin on aika yleistä että heillä on tarjota rahasto, joka on viimeisen parin vuoden aikana pieksänyt viimeisen parin vuoden aikana vertailuindeksit mennen tullen. Mikä kyseisen rahaston menestys on ollut ennen tätä esiteltyä aikajaksoa tai miten heidän kaikki muut rahastot ovat ylipäänsä menestyneet, ei välttämättä olekaan niin suosittu puheenaihe. Sattumaa sisältävissä tapahtumissa havaitaan aina poikkeuksellisen hyviä ja huonoja tapahtumia kun yrityksiä on vaan riittävästi. Pystyvätkö pankin rahastonhoitajat tuottamaan sitten asiakkaalle lisäarvoa pitkällä tähtäimellä? Sitä mitataan aivan muilla tavoilla kuin yksittäistä tähtirahastoa hehkuttamalla valitulla ajanjaksolla.

Takaisin unten maille

Unia tulee ja menee jatkuvasti. Ainakin omien kokemusten mukaan ne aika usein valmistavat tulevaisuuden potentiaalisille ikäville skenaarioille (paisti teini-iässä skenaariot olivat pääasiassa positiivisempia). Huomiota ne herättävät ja muistiin jäävät kuitenkin vain silloin kuin ne oikeasti toteutuvat. Ne sadat ja tuhannet unet jotka eivät koskaan oikeasti toteudu, eivät jää elämään tarinoiksi joita kerromme lapsenlapsillemme.

Statistickon steesit:

Aivomme tykkäävät tarrata yhteensattumiin ja unohtaa ne kerrat kun omat ennustuksemme eivät toteutuneet
Kun joku hehkuttaa ilmiömäisiä ennustuskykyjä, kysy onko kaikki ennustukset huomioitu vai onko ollut mahdollisuus valikoida jälkikäteen hehkutukseen päätyvät
Isoäidit ei valehtele :)

Jalkapalloanalytiikan kulta-aikaa

Posted by :Statisticko On : 10.6.2014

Category: Ennustaminen, Todennäköisyydet, Vedonlyönti

Tags:aineistokritiikki, ennustaminen, jalkapallo, kisaveikkaus, todennäköisyys, vedonlyönti

Näin jalkapallon MM-kisojen kynnyksellä elämme analytiikan kulta-aikoja. Ihmiset laidasta laitaan kiinnostuvat analysoimaan jalkapallojoukkueita ja yrittävät löytää taikakaavaa voittajan ennustamiseen. Työyhteisöjen kisaveikkaukset saavat harvemminkin urheilua seuraavat sukeltamaan hetkeksi veikkausten ihmeelliseen maailmaan. Mutta tästä lisää kirjoituksen lopussa. Katsotaan kuitenkin ensin, kuinka mediassa taho jos toinenkin on valjastanut tilapäisen analytiikkainnostuksen huomion keräämiseen.

Kosmofyysikko jalkapallon pauloissa

Tässä artikkelissa fyysikko Stephen Hawking kokeilee siipiään tilastotieteilijänä analysoimalla Englannin menestymismahdollisuuksia edellisten maailmanmestaruuskisojen perusteella. Hänen tutkimustuloksensa paljastaa mm. seuraavaa Englannin menestymiseen liittyen:

Englannin kannattaa käyttää punaisia paitoja valkoisten sijaan
Taktiikka ”4-3-3” toimii taktiikkaa ”4-4-2” paremmin
Eurooppalainen tuomari parantaa voittotodennäköisyyttä eteläamerikkalaiseen verrattuna
Korkealla pelaaminen murskaa Englannin voittomahdollisuudet

Olipa Hawkingin saavutukset fysiikan saralla kuinka kovat tahansa, niin tilastotieteilijänä on vielä petraamisen varaa. Jo tuon lehtiartikkelin perusteella hän onnistuu sortumaan useaan aloittelijan virheeseen analyysissaan. Toki näiden lehtijuttujen ensisijainen tarkoitus on tarjota vain ”höpöhöpö”-viihdettä, mutta koska juttuun on sotkettu oikea tiedemies, yritetään avata joitain ilmenneitä hämäryyksiä ja selviä virheitä:

Valikoitu aineisto? Aineistona on MM-vuodesta 1966 lähtien. Miksi juuri tähän on aineisto rajattu? Eihän vaan Englannin kotikisoilla 1966 ole jotain tekemistä ”valinnan” kanssa?
Aineiston käyttökelpoisuus?”Logistinen regressio” on varsin etevä analyysityökalu monien todennäköisyyksien mallintamiseen, kun aineistona on nykyhetkenkin populaatiota kattavasti kuvaava satunnaisotos. Kuinka hyvin 1960-luvun joukkue tai MM-kisat ylipäätään kuvaa nykypäivän joukkuetta tai kisoja?
Aineiston koko? Tutkimuksessa on mukana kokonaista 12 turnausta (kisojen lukumäärä vuodesta 1966 alkaen). Jos Englanti pelaisi keskimäärin 5 ottelua turnauksessa, olisi tutkimuksen otoskoko 60. Aineiston riittävyys luotettaviin päätelmiin riippuu paljon siitä, kuinka montaa eri muuttujaa on tarkoitus tutkia. Jos huomioidaan vaikka pelkästään mainitut kolme luokittelevaa tekijää (puna/valkea pelipaita, ”4-3-3″/”4-4-2” taktiikka, eurooppalainen/etelä-amerikkalainen tuomari), jakautuu aineisto 2 * 2 * 2 = 8 osaan. Jokaiseen osioon jää siis keskimäärin 60 / 8 = 7.5 havaintoa. Pelipaidan väri tuskin on kuitenkaan ollut tutkimuksen pääkohde vaan haiskahtaa, että tässä on tutkittu lisäksi hyvin monia muitakin muuttujia, mutta nämä ovat nyt tällä kertaa sattuneet putkahtamaan esiin.

Tutkimuslöydöksiin liittyvästä epävarmuudesta ei artikkelissa puhuttu mitään, mutta ei tarvitse olla Einstein (Hawkingin esikuva) arvatakseen, ettei se taida kestää päivänvaloa.

Jalkapallovedonlyönti – kuin rahaa laittaisi pankkiin?

Toinen vastaantullut yritys on maailman mahtipontisimman pankin Goldman Sachs tekemät ennusteet. Tässä tutkimuksessa on päästy eroon monista Hawkingin ongelmista ottamalla mukaan kaikki muutkin maaottelut kuin MM-kisat lähes sadan vuoden aikana. Joukkueiden tasoerojen muutoksia on pyritty kontrolloimaan edeltävien pelien avulla automaattisesti joukkeiden taitotasoa pisteyttävällä ELO-menetelmällä. Lisäksi tutkimuksessa on pelipaitojen värin sijaan keskitytty oleellisiin muuttujiin.

Koneisto antaa paljon ihan uskottavan suuruisia arvioita, mutta esim. Brasilia saa pelottavan suuria todennäköisyyksiä: tutkimuksen mukaan Brasilia tulee voittamaan kotikisansa 50% todennäköisyydellä. Tutkijat lopussa myöntävätkin, että heidän käyttämämä ELO-pisteytys korostaa mahdollisesti liikaa aivan viimeisiä tuloksia ja Brasilialla sattuu olemaan juuri nyt alla suurinumeroiset voitot kovista maista viime kesältä( 3-0 vs. Espanja ja 4-2 vs. Italia). Lisäksi tutkimuksen mallissa on suuri painoarvo MM-kisojen kotiedulla, minkä voisi epäillä hieman laimenneen historian saatossa, vaikka 1930-1970-luvuilla nähtiinkin paljon kotimestaruuksia.

Kyseessä on sinällään mielenkiintoinen ja kunnianhimoinen yritys mallintaa tilastollisin menetelmin todennäköisyyksiä ilman syvällistä jalkapallo-osaamista. Tutkijat oikeaoppisesti myös testaavat menetelmän tomivuutta vuoden 2010 kisojen otteluihin ennen sitä tunnettujen tietojen avulla ja tulevat siihen lopputulokseen, että sattumalla on hyvästä analyysista huolimatta suuri vaikutus lopputuloksiin. Firman kannattaa siis edelleen keskittyä jauhamaan rahaa pankkibisneksillään. Internetin vedonlyöntimarkkinoilla vahvimmilla ovat ne, jotka historiadatan hallitsemisen lisäksi osaavat muuttaa numeroiksi yksittäisten pelaajien taitotasot ja joukkueen pelitaktiikan sekä yhteensopivuuden vastustajan taktiikkaa ja pelaajia vastaan. Nykypäivänä menestyvä vedonlyönti on siis yhdistelmä pitkälle vietyä lajituntemusta ja tilastotiedettä.

Itselläni ei futistietämys riitä vedonlyöntimarkkinoilla riittävän hyvään todennäköisyyslaskentaan, mutta sen sijaan osaan hyödyntää joitain vedonlyöntimarkkinoilla olevia tehottomuuksia. Näistä kiinnostuneiden kannattaa olla hereillä Twitterissä lähipäivinä.

Statistickon steesi:

Tilastomenetelmien turvallinen käyttö vaatii tutkittavan aiheen sisältöosaamista ja aineiston soveltuvuuden kriittistä arviointia

Bonussteesit työporukkaveikkauksiin (ei vielä tieteellisesti todistettuja):

Maalien tarkkuudella annetuissa tulosveikkauksissa yllätykset osuvat liian harvoin. Todennäköisin lopputulos on yleensä aina ’1-1’, mikäli ottelu on vähääkään tasaväkinen. Jos toinen joukkue on selvä suosikki, kannattaa veikata ’1-0’ ja murskasuosikille ’2-0’
Kannattaa valita yksi ”idea-joukkue”, jolla on hyvät mahdollisuudet päästä pitkälle, mutta jota muut kisan veikkaajat eivät ehkä osaa arvata. Nyt potentiaalinen musta hevonen voisi olla jokin vähemmän tunnettu Etelä-Amerikan maa kuten Uruguay, Kolumbia tai Chile.
Pääasiassa kannattaa suosia todennäköisiä menestyjiä ja lopputuloksia, mutta pelkkiä yleisiä suosikkeja veikkaamalla on vaikea nousta veikkauksen kärkiryhmästä voittajaksi. Sen takia voittaja tarvitsee ripauksen tuuria ”idea-joukkueensa” onnistumisen muodossa.

Tuurin alkulähteillä

Posted by :Statisticko On : 9.5.2014

Category: Ennustaminen, Epävarmuus, Todennäköisyydet

Tags:ennustaminen, epävarmuus, nopanheitto, säkä, sääennuste, todennäköisyys, tuuri

Kirjoitus on julkaistu myös Louhia-blogissa 9.5.2014.

Tilastotieteeseen perustuva analytiikka on jollain tapaa säännönmukaisuuksien ja sattuman erottelua toisistaan. Vastasyntyneen lapsen isää saattaa kiinnostaa, minkä tietojen avulla voidaan laskea lapselle odotettu pituus aikuisiässä (ohjatakseen ajoissa oikean urheilulajin pariin) ja millä todennäköisyydellä pituusennuste menee täysin pieleen. Pokerinpelaajaa saattaa kiinnostaa oliko turnauksen voitto pääosin vain tuurin ansiota vai oliko hän oikeasti muita parempi pelaaja.

Sattuman määrittelyä noppaleikein

Stokastiikka tarjoaa omat matemaattiset perusteet sattumalle, mutta mietitään mitä käytännössä sattuma tarkoittaa. Leikitään, että olemme heittämässä noppaa ja tavoitteenamme on saada heitettyä numero 6. Mietitään tavoitteen onnistumista heitettäessä neljältä eri korkeudelta.

Heitto	Heittokorkeus	Heittotyyli	Todennäköisyys kuutoselle
1.	1 cm	Täysin hallittu pudotus. Sattuma ei ehdi vaikuttamaan.	100%
2.	2 cm	Halittu pudotus, jonka ilmavirta joskus kääntää väärään numeroon	75% (arvio)
3.	5 cm	Suljetaan 2 numeroa pois heittämällä niin, että noppa pyörii vain yhteen suuntaan	25% (=1/4)
4.	100 cm	Täysin sattumanvarainen	16.7% (=1/6)

Jossain välillä 5 cm – 100 cm olemme ylittäneet rajan, jonka jälkeen emme enää pysty heittotaidoilla vaikuttamaan kutosen ilmenemiseen. Ilmanvastuksen ja painovoiman vaikutus on sellainen, jota emme osaa hallita/laskelmoida, joten meidän näkökulmasta sattuma määrää täysin lopputuloksen. Todennäköisyysjakaumat määrittävät kuitenkin raamit, missä sattuma operoi. Tässä tapauksessa todennäköisyysjakauma sanoo, että kutonen tulee kerran kuudesta, eli todennäköisyys on 16.7%.

Näin saatiin hahmoteltua sattumalle (= tuurin/säkän vaikutus) käytännönläheinen määritelmä: Sattuma on informaatiota, jota ei tunneta. Kun noppa on pysähtynyt, tiedämme tuloksen eikä tulokseen ole enää sattumalla vaikutusta. Nopan ollessa ilmassa osa lopputuloksen informaatiosta on vielä tuntematonta. Sen määrä riippuu siitä, miltä korkeudelta kutosta yritetttiin tähdätä.

Sattuman tyypit

Tässä vaiheessa jakaisin sattuman vielä kahteen luokkaan.

B-luokan sattuma
Sattumaa, joka on jonkinlaisella tietotaidolla supistettaavissa. Esim. kohdan 2. nopanheitossa joku taitava heittämistä harjoitellut taikuri saattaisi saavuttaa kutosen todennäköisyyden 98%, vaikka meillä tavallisilla viskelijöillä se oli 75%.

A-luokan sattuma
Sattuma, josta ei millään päästä eroon vaikka käytettävissä olisi kaikki tämän hetken tietotaito ja teknologiat. Esim. noustaan Puijon torniin heittämään noppaa maahan, niin ei varmasti maailmasta löydy sellaista taikuria, joka pystyisi nostamaan kutosen todennäköisyyttä yli 16.7%:n. (Noppaan ei saa tehdä fyysisiä muutoksia.) Näin ollen kaikki heittoon liittyvä sattuma on A-luokan sattumaa.

Ennusteiden subjektiivisuus

Nyt olemme ehkä jo havainneetkin, että sattuma voi olla jossain määrin subjektiivinen (vaihtelee eri henkilöiden välillä) käsite. Havainnollistetaan sitä vielä seuraavalla esimerkillä:

Kolme henkilöä yrittää ennustaa (omilla tiedoilla, ilman netin tai TV:n apua), mikä on lämpötila Helsingissä seuraavana päivänä klo 12.

1. Eetu Extremeurheilija

Eetu on ollut onnettomuuden jäljiltä viimeiset puoli vuotta koomassa. Hän on juuri herännyt ikkunattomassa sairaalasssa. Eetulla onneksi aivot toimivat normaalisti, mutta hänellä ei ole minkäänlaista ajantajua edes vuodenajasta. Eetun tekee näillä tiedoilla parhaan mahdollisen arvauksen ja veikkaa edellisten vuosien arvioitua keskilämpötilaa +7 astetta. Eetu tosin tiedostaa, että arvauksessa on paljon epävarmuutta ja sattumalla on iso vaikutus siihen, kuinka lähelle ennuste osuu.

2. Pera Perustietäjä

Peralla ei ole käytössä analyysimenetelmiä, joista voisi olla hyötyä tarkkojen ennusteiden tekemiseen. Hän kuitenkin järkeilee, että peräkkäiset päivät ovat yleensä jossain määrin samankaltaisia. Omien tietojensa pohjalta hänen paras arvaus onkin tänään päivällä lämpömittarissa paistanut lukema +20.

3. Mauno Mallintaja

Mauno on maailman parhaimmistoon kuuluva metereologi. Hänellä on tiedossa ilmakehän muutoksien systematiikka ja hän osaa hyödyntää monimutkaista matematiikkaa sisältäviä malleja lämpötilojen ennustamiseen. Hän vastaa ennusteeseensa perustuen +15 astetta ja osaa kertoa myös että 95% varmuudella lämpötila on välillä +12 ja +18 astetta.

Katsotaan sitten todennäköisyysjakaumien avulla, miltä ilmiö nimeltä ”huomisen lämpötila” näyttää itse kunkin näkökulmasta. Näissä kuvioissa jakauman leveys kuvaa arvauksen liittyvää sattuman määrää ja toisaalta kuvion korkeus ennusteen hvyyyttä kyseisessä kohdassa.

Maunon ennusteeseen liittyy pelkästää A-tyypin sattumaa, koska hänellä on käytössä kaikki tämän hetken tietotaito ja parhaat analyysimenetelmät. (Tilanne voi olla toinen esim. viiden vuoden päästä teknologian kehittyessä). Peralla ja Eetulla ennusteeseen liittyy A-luokan sattuman lisäksi B-luokan sattumaa. Osan Eetun B-luokan sattumasta Pera onnistui mallintamaan hyödyntämällä tietoa tämän päivän lämpötilasta. Peran B-luokan sattuman taas Mauno mallinsi pois hyödyntämällä tietoa ilmavirtojen liikehtimisestä. (Jäljelle jääneen sattuman määrä näkyy punaisen epävarmuusjakauman leveytenä.)

Seuraavana päivänä ennustuskisa ratkesi ja tulos oli 17 astetta. Lähimmäksi osui Mauno, mikä oli odotettavissakin. Tosin Perankin ennuste heitti vain 3 astetta. Mikäli muut eivät tietäisi Maunon metereologi-taustasta, saattaisi hän helposti saada jälkipeleissä ”Hannu Hanhi” -lisänimen.