Rss

  • linkedin

Archives for : Algoritmit

Päätöksiä ristiriitaisten tavoitteiden maailmassa

Posted by :Statisticko On : 20.3.2024
0

Category: Algoritmit, Liiketoiminta, Päätöksenteko

Tags:, , , , , ,

”Haluan ostaa asunnon, joka olisi hyväkuntoinen ja sijainti on keskeinen, mutta asuinalueen pitäisi olla rauhallinen. Hinnan pitäisi myös olla edullinen.”

”Perheellemme pitäisi löytää lomakohde, josta löytyy mielenkiintoista tekemista isälle, äidille ja lapsille. Reissu ei saisi olla kuitenkaan kohtuuttoman kallis.”

”Haluan sijoittaa rahani niin että varallisuuteni kasvaisi mahdollisimman suureksi, mutta rahan häviämisen riski olisi mahdollisimman pieni.”

Yllä olevat kommentit kuvaavat erilaisia valintatilanteita, missä on useampi kuin yksi tavoite. Lisäksi tavoitteet ovat ainakin osittain ristiriitaisia. Tämä tarkoittaa sitä ettei ole olemassa sellaista ratkaisua, joka olisi optimaalinen kaikkien tavoitteiden suhteen. Joudumme siis etsimään kompromisseja.

Kompromissiloma

Toisessa kommentissa isän unelmaloma voisi olla Valioliiga-ottelun näkeminen Liverpoolissa, äidin surffausloma Balilla ja lapset haluaisivat Disney Worldiin. Kompromissivalinta voisi olla esimerkiksi Malaga, missä pääsee katsomaan Espanjan jalkapalloliigaa, löytyy merenranta surffaukseen (vaikkei aallot vastaakaan Balia) sekä vesipuisto lapsille. Jokaisen perheenjäsenen tavoitteessa jouduttiin hieman antamaan periksi. Silti valinta tyydyttää kaikkia ja budjetti on vanhemmille miellyttävämpi kuin Euroopan ulkopuolisissa kohteissa. Tämän tyyppisiä valintatilanteissa turvaudutaan monitavoitteiseen (tai monikriteeriseen) päätöksentekoon.

Kun useat tavoitteet vetävät eri suuntiin, pitää löytää paras mahdollinen kompromissi

Varaston optimointia

Sen kunniaksi että ikuisuusprojektin viittaa kantanut toinen väitöskirjaani tuleva artikkeli vihdoin syksyllä julkaistiin, käyn tässä läpi monitavoiteoptimointia artikkelissa olevan sovelluskohteen näkökulmasta. Kyseessä on yrityksen varaston optimointiongelma: päätöksentekijänä on ostopäällikkö, jonka pitää päättää kuinka paljon tilataan varastoon alihankkijalta tavaraa, jonka toimitusaika on 3 kk. Kyseessä oli teollisuusyritys ja tilattava tavara oli kallis komponentti, jota tarvitaan lopputuotteen valmistamiseen. Matematiikka kuitenkin täsmää vaikka tavara olisi tukkukauppiaalta tilattava valmis tuote jälleenmyytäväksi.

Yrityksen ostotoimintoihin ja varaston ylläpitöön liittyy useita kustannuksia. Esimerkiksi kuljetuskustannukset, pääomakustannukset (yrityksen varoja sitoutuu varaston tuotteisiin) ja tuotteiden vanheneminen/pilaantuminen. Mikäli ostopäällikkö pelkästään minimoisi kustannuksiaan, hänen ei koskaan kannattaisi tilata mitään. Ikävänä sivuseurauksena silloin yrityksen liiketoimintakin loppuisi kun ei ole mitään myytävää.

Ostopäällikon ongelma on siis seuraava:

– jos hän tilaa usein / paljon tavaraa varastoon, kustannukset nousevat pilviin

– jos hän tilaa liian vähän, kaikille asiakkaille ei riitä lopputuotetta myytäväksi.

Ostopäällikön liian suuret tilaukset aiheuttavat säpinää varastossa

Eräs ratkaisu on arvioida, mikä kustannus yritykselle tulee yhdestä pettyneestä asiakkaasta ja lisätä tämä muihin varastointikustannuksiin, jolloin tilauspäätös voitaisiin tehdä kaikkia näitä kustannuksia minimoimalla. Nyt oleellisia kysymyksiä ovat:

– Kuinka paljon yksi pettynyt asiakas pitkällä tähtäimellä maksaa?

– Onko yrityksen brändiarvon heikkeneminen lineaarista vai onko 5:n peräkkäisen pettymyksen hinta suurempi kuin 5 kertaa yksi pettymys?

Sen sijaan että ravistelee hihasta euromääräisen hinnan asiakkaan pettymykselle, on mahdollista mitata ajallaan palveltujen asiakkaiden määrää omalla mitta-asteikollaan. Eli ei yritäkään muuttaa asiakkaiden kokemia pettymyksiä Euroiksi. Tästä pääsemmekin monitavoiteoptimoinnin maailmaan.

Kahden tavoitteen optimointi yhtäaikaa

Nyt meillä on päätöksenteolle kaksi tavoitetta:

1. varastointikustannusten minimointi

2. asiakkaiden palvelutason maksimointi

Nämä ovat ristiriitaisia tavoitteita, koska ensimmäisen tavoitteen kannalta pitäisi tilata varastoon mahdollisimman vähän ja toisen kannalta mahdollisimman paljon. Sopivan kompromissin löytämisen avuksi tulee käsite Pareto-optimaalisuus.

Tutkimuksessa ostopäällikön ostostrategiassa käsiteltiin kolmea aikapistettä yhtäaikaa: kuinka paljon tilataan ensimmäisessä mahdollisessa erässä, kuinka paljon seuraavassa ja kuinka paljon sen seuraavassa. Yhden eräkoon vaihdellessa välillä 0-250 kpl, mahdollisia kombinaatioita on 251^3 = 15813251 kpl. Otetaan tässä kuitenkin käsittelyyn hieman yksinkertaistettu kuvitteellinen esimerkki, missä eräkoko voi vaihdella välillä 0-9, jolloin kombinaatioita on ”vain” 1000 kpl. Ne on kuvattu pisteinä alla olevassa koordinaatiossa. Tässä esimerkissä oletetaan 100€ kiinteä kuljetus- ja käsittelykustannus aina kun tilataan nollaa suurempi erä.

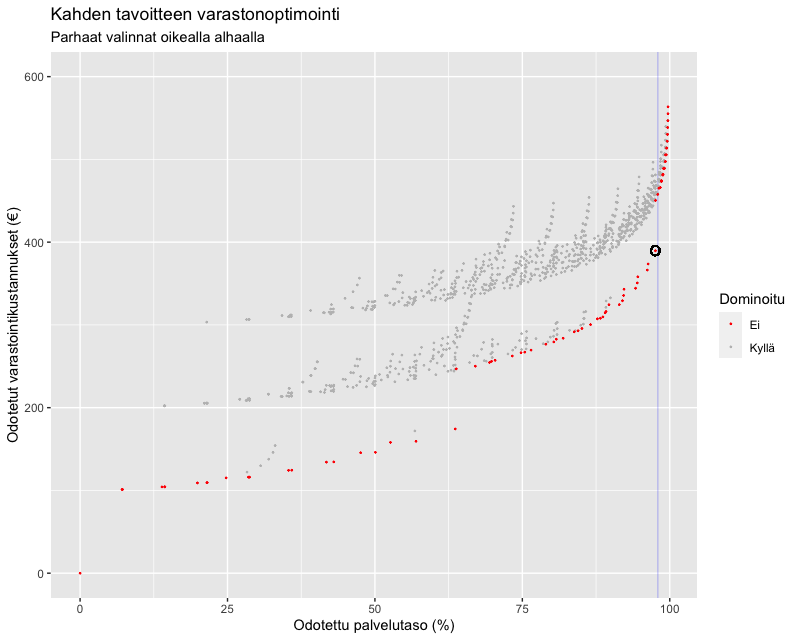
Kuvaajassa vaaka-akselilla on odotettu palvelutaso (kuinka suuri %-osuus kysynnästä saadaan ajallaan tyydytettyä) ja pystyakselilla odotetut kustannukset eri tilausmäärä-valinnoilla. Hyvät vaihtoehdot sijaitsevat alhaalla oikealla, mutta mikä valinnoista on paras? Tähän ei ole yksiselitteistä vastausta, mutta sen sijaan me osaamme sanoa, mitkä eivät ainakaan ole parhaita. ”Harmaiden pisteiden sanotaan olevan dominoituja, koska yhden tavoitteen parantamiseksi ei toisesta tavoitteesta tarvitse tinkiä.”

Sen sijaan punaisia pisteitä ei ole dominoitu. Mikäli punaista ratkaisua haluaa parantaa yhdessä tavoitteessa, on pakko heikentää toista tavoitetta. Näitä punaisia ratkaisuja sanotaan Pareto-optimaalisiksi. Ostopäällikön tehtäväksi jää näistä Pareto-optimaalisten ratkaisujen joukosta löytää näkemystään hyödyntäen sopivin kompromissi.

Jos viime aikoina on usealle asiakkaalle jouduttu myymään ”ei oota” ostopäällikkö saattaisi nyt pelata varman päälle ja tavoitella lähelle 100% olevaa palvelutasoa. Lopullinen valinta voisi olla ympyröity piste. Tällä valinnalla odotettavissa on 97.6% palvelutaso (vaaka-akseli) ja 390 euron (pystyakseli) varastointikustannukset. Siihen päästään kun tilataan varastoon ensimmäisessä erässä 9, toisessa 9 ja kolmannessa 0 tuotetta.

Tämä esimerkki kuvaa myös eroa monitavoiteoptimoinnin ja rajoitetun optimoinnin välillä. Mikäli ostopäällikkö olisi määrittänyt rajoitteeksi 98% palvelutason (sininen pystyviiva) ja minimoinut sitten pelkästään kuluja, hän olisi päätynyt pystyviivan oikealla puolella olevaan ratkaisuun. Siten hän ei olisi koskaan saanut tietää että vain 0.04%-yks. pudotuksella 98% tavoitteesta pystyi saamaan merkittävän n. 70€ säästön. Tätä säästöä selittää 100€ säästö kuljetus- ja käsittelykutannuksissa kun kolmas tilauserä jätetään nollaksi.

Ratkaisujen laskeminen

Kun mahdollisia päätöksiä (tai päätöskombinaatioita) on miljoonia tai jatkuvien muuttujien tapauksessa rajaton määrä, kaikkien mahdollisten ratkaisujen laskeminen veisi aivan liian paljon aikaa myös nopeimmilta tietokoneilta. Niinpä on kehitetty laskenta-algoritmeja, jotka etsivät pelkästään Pareto-optimaalisia ratkaisuja päätöksentekijän toiveiden mukaisesti. Algoritmeja on paljon erilaisia erilaisiin sovelluksiin, mutta tunnetuin yleiskäyttöinen algoritmi lienee NSGA (Non-dominated Sorting Genetic Algorithm).

Vielä lisää tavotteita

Tavoitteiden määrä ei välttämättä rajoitu kahteen. Tutkimuksessa ostopäälliköllä oli vielä kolmaskin tavoite: varaston kiertonopeus (=kuinka usein tavara vaihtuu varastossa). Vaikka kiertonopeus korreloikin varastointikustannuksen kanssa, se tuo tärkeää lisäinformaatiota ostopäällikölle. Mikäli kiinteät kuljetus- ja käsittelykustannukset ovat korkeat, kustannusten minimointi suosii isoja kertatilauksia. Isot tilausmäärät kuitenkin pienentävät varaston kiertonopeutta tuottaen käytännön ongelmia varastotilojen riittävyyteen, varastotyöntekijöiden työturvallisuuteen ja nostavat riskiä että tuotteet vanhenevat varastoon.

Vaikka kolmen tavoitteen pohjalta muodostettu Pareto-optimaalisten ratkaisujen joukko on hankalampaa (ja neljän tavoiteen mahdoton) visualisoida koordinaatistossa, monitavoiteoptimointialgoritmit kyllä hoitavat Pareto-optimaalisten ratkaisujen etsimisen samoin kuin kahden tavoitteen tapauksessa.

Kysynnän ennustaminen

Päätöksentekijällä on vielä yksi ongelma. Tavoitteiden laskemiseen tarvitaan tietoa tulevien kuukausien kysynnästä lopputuotteelle, mutta yleensä tätä ei varmaksi tiedetä etukäteen. Sen sijaan historiadatan avulla pystymme arvioimaan todennäköisyyksiä erilaisille kysyntäskenaarioille. Tähän sukellamme tarkemmin jossain toisessa blogikirjoituksessa, mutta mikäli asia kiinnostaa voit tutustua tähän kaikkeen lukemalla itse artikkelin. Virallinen julkaisu löytyy maksumuurin takaa täältä, mutta yliopistolla on myös ilmainen rinnakkaisjulkaisu vähemmän viimeistellystä versiosta, joka löytyy täältä.

Yhteenveto

Yksi tapa kuvata monitavoitteista päätöksentekoprosessia on Daniel Kahnemanin populariosoiman kahden ajattelusysteemin (lue esittely esim. täältä) yhdistäminen. Ensiksi käytetään hidasta, eli 2-systeemin, ajattelua määrittelemällä päätökseen hyvyyteen vaikuttavat tavoitteet. Laskenta-algoritmeja hyödyntämällä näiden tavoitteiden perusteella karsitaan huonot vaihtoehdot pois. Jäljelle jääneistä Pareto-optimaalisista vaihtoehdoista tehdään lopullinen valinta nopeaa, eli 1-systeemin, ajattelua hyödyntäen. Näin saadaan sulavasti tietokoneen laskentateho sekä ihmisen näkemys ja intuitio tekemään yhteistyötä tilanteeseen sopivan kompromissin etsimisessä.

Facebooktwitterredditpinterestlinkedinmail

Kelly-vetoja osakkeiden maailmassa

Posted by :Statisticko On : 22.12.2020
1

Category: Algoritmit, Osakesijoittaminen, Päätöksenteko, Riskien hallinta, Tutkimukset

Tags:, , , , ,

Pian päättyvä vuosi on ollut sekä tämän blogin että lähes kaiken muunkin vapaa-ajan aktiviteetin osalta aika hiljainen. Suurin yksittäinen selittäjä pandemian lisäksi tälle on se että tämä vuosi päättää seitsemän vuotta sitten alkaneen taloustieteen opiskeluun liittyvän opinto-oikeuden. Vuosi on sisältänyt paljon pitkiä iltoja gradun parissa. Nyt kyseinen apina on selästä pudotettu ja tässä kirjoituksessa kerron mitä iloa graduni voisi muillekin tuottavaa.

Gradun salainen taka-ajatus on ollut kehittää itselleni työkalua, jonka avulla voisin hahmotella sopivaa riskinoton määrää eri sijoituskohteille osakemarkkinoilla. Kun työn kokonaisuus alkoi hahmottumaan, huomasin että tämähän on aika hyvä lähestymistapa sijoittamiseen kelle tahansa satunnaisesti osakesijoittamista harrastavalle.

Romahduksia tulee, mutta ei hävitetä silloin kaikkia palikoita

Vanhana urheiluvedonlyöjänä Kellyn kriteeristä on muodostunut standardi riskinhallinan työkalu. Tässä kirjoituksessa aiemmin jo avasin Kellyn kriteerin saloja yksinkertaisessa vedonlyönnissä. Lyhyesti tavoitteena on maksimoida pitkällä ajanjaksolla varallisuuden kasvuvauhti ilman että missään välissä menee konkurssiin. Gradussa pyrin tarjoamaan yhden ratkaisun Kellyn kriteerin käytännön hyödyntämiseen osakemarkkinoilla, mikä aiheuttaa kipuilua koska osakkeiden tulevaisuuden tuottojen luotettava kuvaaminen matemaattisesti ei ole mikään helppo nakki. Opinnäytetyön pyrin kirjoittamaan tieteelliseen muottiin ja siihen voi tutustua täällä. Nyt blogikirjoituksessa kuitenkin otan vapauden puhua sijoittamisesta vapaasti omien näkemysten mukaan.

Satunnaiselle säästäjälle/sijoittajalle markkinan keskituoton tavoittelu laajasti hajauttavan indeksirahaston avulla on järkiratkaisu. Myös graduni sijoitusstrategiassa indeksi on pääsijoituskohde ja tärkein ratkaistava asia on päättää kuinka suuri osuus omaisuudesta on kiinni osakeindeksissä ja kuinka paljon “riskittömässä” korossa, eli nykyään käytännössä käteisessä.

Mitä tulee markkinoiden tehokkuuteen, itse näen asian subjektiivisena asiana. Kaikista näppärimmät ja nopeimmat hyvin informoidut kaverit pystyvät tekemään systemaattista ylituottoa ja elättämään itsensä käymällä pörssikauppaa. Mutta juuri näiden kavereiden kaupankäynti ajaa hintoja sellaiselle tasolle, että keskivertosijoittajalle markkinat näyttäytyvät varsin tehokkaina. Vaikka tavalliselle päivätyössä käyvälle sijoittajalle suurimmassa osassa yrityksistä on liian vaikea hankkia informaatioetua markkinoihin, minussa asuu kuitenkin ripaus Peter Lynchmäistä optimistisuutta. Mikäli herran kirjallisuus ei ole tuttua, voit aloittaa tutustumisen vaikka tästä Inderesin podista.

Lynchin ydinajatus on että kuka tahansa voi saavuttaa informaatioetua osakesijoittamissa sellaisten yritysten tai toimialojen kohdalla, joiden parissa viettää joka tapauksessa paljon aikaa esimerkisi työn tai harrastuksen takia. Esim. jos työskentelet auton osia valmistavassa firmassa ja toimitat tavaraa usealle kilpailevalle auton valmistajalle, voit olla hajulla siitä millä valmistajalla tänä vuonna myynti kiihyttää eniten ennen kun virallisten raporttien tieto menee ammattianalyytikoille. Tai vaikka intohimoisena peliharrastajana voit olla ensimmäisten joukossa hajulla, minkä firman uudesta pelistä tulee seuraava jättihitti. Kyse on yksinkertaisesti siitä, että pitää tietää jotain tärkeää, mitä suurin osa muista sijoittajista ja analyytikoista ei vielä tiedä.

Vaikkei työskentelisikään sellaisella alalla, missä voisi saada informaatioetua, suora sijoitus yksittäiseen osakkeeseen on perusteltua myös oppimisprosessin ja mielenkiinnon ylläpidon takia. Itselläni osakesijoittamisen aloittaminen vuonna 2009 sytytti aivan uudenlaisen uteliaisuuden kipinän ympärillä pyörivää yhteiskuntaa kohtaan. Uteliaisuus johti lopulta vuonna 2013 taloustieteen opiskelun aloittamiseen ja nyt lopultakin tämän gradun valmistumiseen. Joten olkaahan varovaisia siellä!

Sijoitusmaailmasa vain epävarmuus on varmaa, joten sijoitussalkun runko on hyvä perustaa hajautettuun indeksiin vaikka yksittäisessä firmassa olisikin erittäin hyvin hajulla. Gradussa kehittämässäni algoritmissa riskittömän koron ja osakeindeksin lisäksi on mahdollista sijoittaa myös yhteen yksittäiseen osakkeeseen. Rajaus yhteen johtui puhtaan teknisistä syistä: useamman osakkeen käsittely yhtäaikaa vaatisi myös näiden välisen riippuvuuden mallintamisen (mikä ei selity yleisellä markkinakehityksellä) ja olisi lisännyt työmäärää, mitä riitti näinkin ihan tarpeeksi. Käytännössäkin keskivertosijoittajalla ei voi olettaa olevan kovin montaa oikeasti hyvää sijoitusideaa kerrallaan, joten sen puolesta ehkä on vain hyvä ettei laita paljoa paukkuja kuin parhaaseen ideaansa.

Vaikka tavoiteltavan sijoitustyökalun ideana on käyttäjän itse antaa yksittäiseen osakkeeseen liittyvää omaa “erikoistietämystä”, gradussa yksittäisen osakkeen näkemys pohjautuu analyytikoiden tavoitehintoihin. Tällä hetkellä työkalusta on julkaistu demoversio, mikä noudattaa täysin gradun kaavoja ja antaa tehdä sijoituspäätöksen 31.12.2019 olleilla tiedoilla 20 vuoden historiaan ja sen hetken analyytikoiden tavoitehintoihin pohjautuen. Sijoituskatalogissa valikoimassa on käteinen, Helsingin pörssin osakeindeksi ja valtionyhtiöitä (väh. 10% omistus), joilta on historiadataa 20 vuoden ajalta. Työkaluun voi tutustua täällä.

Ennen kuin teet sijoituspäätöksiä työkalun perusteella on hyvä tiedostaa, että älä tee. Ainakaan pelkästään sen avulla. Käytän hintojen mallintamisessa t-jakaumaa, mikä on paksuhäntäisenä normaalijakaumaa huomattavasti parempi vaihtoehto. Mutta mikäli on Talebinsa lukenut, tietää ettei osakkeiden tuottojakaumien häntien kanssa ihan näin helpolla selviä ja sellaisia ikäviä yllätyksiä on odotettavissa, mihin pelkästään historiadatan avulla ei pystytä varautumaan. Mikäli tämä tai muut mallin yksityiskohdat kiinnostavat, niistä voi lukea lisää gradusta. Tässä kohtaa on oleellista tietää, että työkalu sopii lähinnä omaan riskinsietokykyyn sopivan osakeriskin ylärajan hahmottelemiseen. Käytännössä mustien joutsenien takia riskit kannattaa pitää työkalun suositusta alemmalla tasolla. Kehitystyö varmasti jatkuu, näillä näkymin myös tieteellisen julkaisun muodossa, ja kehitysideoita otan ilomielin vastaan.

Bayes-Kelly osakeportfolion optimointistrategia pähkinänkuoressa:

1. Valitse yksi osake riskivapaan koron ja indeksisijoituksen lisäksi (tai tyydy pelkkään indeksiin)

2. Valitse itsellesi sopiva turvarajoite = “hyväksyttävä vuosittainen tappio prosentteina sijoitusvarallisuudesta”

3. Optimoidaan eri kohteisiin sijoitettavat osuudet varallisuudesta niin että pitkän tähtäimen (tästä hetkestä ikuisuuteen) odotettu varallisuuden kasvuvauhti maksimoituu ja todennäköisyys kohdata yksittäisenä vuonna suurempi tappio kuin turvarajoite on alle 5%.

Tästä pääsee leikkimään työkalun mvp demolla ja tästä lukemaan gradua.

Facebooktwitterredditpinterestlinkedinmail

Analytiikan alalajit

Posted by :Statisticko On : 20.6.2019
0

Category: Algoritmit, Ennustaminen, Liiketoiminta, Päätöksenteko

Tags:, , , , , ,

Sijoittajamestari Ray Dalio kokosi elämässään oppimansa asiat teokseen Principles ja päätökseen tekoon liittyvä ensimmäinen periaate kuuluu näin:

”Recognize that 1) the biggest threat to good decision making is harmful emotions, and 2) decision making is a two-step process (first learning and then deciding).”

Ray Dalio

Datan analysointi tai datatieteily liityy nimenomaan ympäristöstä oppimiseen ilman tunteiden aiheuttamia vääristäviä tunteita niin että voitaisiin tehdä mahdollisimman valistuneita päätöksiä.

Kun tehdään liiketoimintaa tukevaa analyysiä, datan analysointi jaetaan tyypillisesti neljään alalajiin riippuen, mitä työllä tavoitellaan. Eri konsultit voivat järjestellä ne hieman eri tavoilla, mutta itse mielelläni järjestäen ne seuraavasti analyyttisen haastavuuden mukaan helpoimmasta vaikeimpaan:

  1. Kuvaileva analytiikka (Mitä tapahtui?)
  2. Ennakoiva analytiikka (Mitä tulee tapahtumaan?)
  3. Diagnosoiva analytiikka (Miksi jotain tapahtui?)
  4. Ohjaileva analytiikka (Mitä kannattaisi tehdä?)

Kolme ensimmäistä liittyy oppimiseen ja viimeinen päätöksentekoon opitun pohjalta.

Hukkuvat jäätelönsyöjät

Avataan sitten näitä alalajeja esimerkin avulla. Hukkuvat jäätelönsyöjät on monelle jo liiankin tuttu esimerkki riippuvuussuhteista, mutta ratsastetaan nyt vielä kerran sillä, koska se kaikessa tomppeluudessaan kuitenkin hyvin demonstroi oleellisia pointteja.

Olkoon meillä toimeksiantona jäätelökioskiyrittäjän auttaminen ja myyntiä ilmiönä kuvaa seuraava graafi.

Lämpötilan nousu aiheuttaa enemmän sekä jäätelön myyntiä että hukkumiskuolemia. Hukkumisen ja jäätelön myynnin välillä ei ole syy-seuraus-yhteyttä.

Graafissa olevien syy-seuraus-yhteyksien pohjalta olen nyt simuloinut 300 havaintoa, jonka kanssa seuraavissa esimerkeissä operoidaan.

Kuvaileva analytiikka

Kuvaileva analytiikka vastaa siis kysymykseen ”Mitä tapahtui?”. Vastaus löytyy raporteista, joissa on tilastollisista tunnuslukuja ja graafisia kuvioita. Yritysmaailmassa tätä analytiikan alalajia kutsutaan termillä Business Intelligence (BI). Meidän dataa 300 aiemmasta viikkohavainnosta kuvaavat esim. seuraavat tunnusluvut.

TEMP (C)SALES (EUR)DROWNED
Keskiarvo19.6130351.15
Keskihajonta5.3413153.52

Lisäksi mielenkiinnon mukaan tunnuslukuja voisi vertailla eri ryhmien, esim. viikonpäivien tai jäätelömakujen, välillä.

Keski- ja hajontalukujen lisäksi havaintoja voi kuvata muuttujien välisillä korrelaatiokertoimilla ja graafisilla kuvaajilla. Seuraava graafi ei ole välttämättä kauneimmasta päästä, mutta minulle sen piirtäminen on osa perusprosessia uuteen aineistoon tutustuttaessa. Siinä on paljon informaatiota tiiviisti ilmaistuna ja sen saa tulostettua R-ohjelmistolla yhdellä komennolla.

Lävistäjällä ovat jokaisen muuttujan omat jakaumat. Vasemmalla alhaalla ovat parittaiset sirontakuviot. Oikella ylhäällä ovat parittaiset korrelaatiokertoimet ja niiden merkitsevyystasot tähtinä.

Kuvaajasta nähdään mm. seuraavaa:

  • Lämpötilan ja myynnin havainnot ovat jakautuneet symmetrisesti keskiarvon ympärille ja muistuttaa normaalijakaumaa. Hukkumisten lukumäärän jakauma on vino.
  • Kaikkien muuttujien väliset korrelaatiokertoimet (luvut oikealla ylhäällä) ovat positiivisia, joten muuttujilla on ollut taipumus saada isoja arvoja yhtäaikaa.
  • Kaikki muuttujien väliset korrelaatiokertoimet ovat tilastollisesti erittäin merkitseviä (punaiset tähdet), joten ei ole uskottavaa että korrelaatiokertoimet poikkeavat nollasta vain sattumalta.
  • Suora viiva kuvaa hyvin myynnin ja lämpötilan välistä yhteyttä. Hukkumisen ja muiden muuttujien välisen yhteyden kuvaamiseen suora viiva ei ole paras mahdollinen (kuviot vasemmalla alhaalla).

Kuvaileva analytiikka keskittyy kuvailemaan historian tapahtumia, mutta vastuu siitä, mitä tulee tapahtumaan tulevaisuudessa jää täysin raportin lukijalle.

Ennakoiva analytiikka

Vaikka historiakin on mielenkiintoista, vielä kiinnostavampaa liiketoiminnan kannalta on se mitä on odotettavissa tulevaisuudessa. Mennyt ei ole tae tulevasta, mutta historiaan perustuen voi tehdä valistuneita arvioita eri tulevaisuuden skenaarioiden todennäköisyyksistä.

Esimerkissämme mielenkiinnon kohteena on ennustaa tulevan viikon jäätelön myyntimäärä. Pelkään BI-raporttiin (kuvaileva analytiikka) perustuen paras arvaus olisi historiallinen keskiarvo 13035 euroa. Simuloin tässä 100 uutta havaintoa tulevista viikoista ja historialliseen keskiarvoon perustuva arvaus ei ole hassumpi: keskimäärin ennuste on 7.3% pielessä.

Olisimme voineet kuitenkin ottaa askel eteenpäin ennakoivan analytiikan puolelle ja muodostaa regressiomalli, jossa hyödynnetään tietoa päivän lämpötilasta. Lämpötilan ja myynnin välinen korrelaatiokerroinhan oli varsin suuri, 0.62. Tällaisen mallin tarjoama paras arvaus seuraavan viikon myynnistä menee nyt uusilla havainnoilla keskimäärin 6.5% pieleen.

Vaikka hukkumisilla ei ole syy-seuraus-suhdetta myyntiin, ei sen hyödyntämiselle ennustamisessa ole estettä. Jos sen lisää toiseksi selittäjäksi samaan regressiomalliin lämpötilan kanssa ei siitä iloa kuitenkaan ole, koska lämpötila jo yksinään selittää hukkumisten ja myynnin välisen yhteyden. Mutta mikäli vahingossa olisimme hukanneet historian lämpötilahavainnot, olisi hukkumiskuolemat hyvä apumuuttuja. Pelkästään edellisen viikon hukkumisiin perustuvat ennusteet ovat tässä tapauksessa 6.7% pielessä. Lopuksi vielä yhteenveto, kuinka tarkasti saatiin 100 uutta myyntihavaintoa ennustetttua.

EnnustajaKeskimääräinen virhe
Oma historia7.33%
Lämpötila6.45%
Hukkumiset6.73%
Lämpötila+Hukkumiset6.43%

Regressiomallien lisäksi muita ennustamisen työkaluja ovat aikasarja-analyysi silloin kun kiinnitetään erityistä huomiota ajassa systemaattisesti toistuviin kuvioihin. Sitten kun käsillä on ajassa stabiili ilmiö, mutta paljon potentiaalisia selittäjiä sekä paljon dataa, arvoon arvaamattomaan nousevat erilaiset koneoppimisalgoritmit kuten neuroverkot tai päätöspuut. Mikäli useiden potentiaalisten selittäjien lisäksi meillä on hieman ymmärrystä näiden selittäjien keskinäisistä riippuuvuussuhteista, voidaan dataa ja asiantuntemusta yhdistää Bayes-verkkojen avulla tai simuloimalla maailman menoa ymmärryksemme rajoissa.

Käyttipä mitä tahansa näistä ennustusmenetelmistä tai jotain niiden yhdistelmää, meillä on kaksi ikävää kiusaa:

  • Ylisovittaminen: tietämättämme yritämme tulevaisuutta ennustaa sellaisilla historiallisilla piirteillä, jotka ovat toteutuneet aiemmin vain sattumalta eivätkä kuvaa ilmiötä tulevaisuudessa. Tätä ongelmaa olen ruotinut aiemmin tässä kirjoituksessa.
  • Pysyvät muutokset muuttujissa, joita ei olla aiemmin mitattu. Esimerkiksi lakimuutokset voivat ohjata ihmisiä käyttäytymään tulevaisuudessa eri tavalla kuin mihin aiemmin olemme tottuneet. Tätä ongelmaa olen käsitellyt tarkemmin tässä kirjoituksessa.

Kiitos mm. edellä mainittujen haasteiden ennakoivassa analytiikassa vaaditaan jo huomattavasti korkeamman tason koulutusta kuin kuvailevassa analytiikassa.

Diagnosoiva analytiikka

Diagnosoivalla analytiikalla pyritään löytämään asioiden välisiä syy-seuraus-yhteyksiä. Tieteellisen uteliaisuuden lisäksi liiketoiminnan kannalta kiinnostavaa voisi olla selvittää, mitä asioita muuttamalla saisimme myyntiä kasvatettua. Ennakoivan analytiikan maailmassa korrelaatiokertoimet antoivat hyviä vinkkejä, mitä muuttujia voisimme hyödyntää ennustamisessa. Kun tavoitteena on puuttua itse peliin asioiden muuttamiseksi, vain korrelaatioita tuijottamalla voisimme päätyä raportoimaan jäätelöyrittäjälle: ”Myynnin edistämiseksi kannattaa alkaa hukuttamaan ihmisiä”. Tämähän ei alkuunkaan pidä paikkansa niinkuin kohta tullaan näkemään.

Varmin tapa syy-seuraus eli kausaaliyhteyden selvittämiseksi on tehdä satunnaisettu koe riittävällä määrällä toistoja. Näistä klassinen esimerkki on antaa satunnaisesti toisille koehenkilöille oikeaa lääkettä ja toisille koehenkilöille lumelääkettä. Vaikutuksia vertailemalla voidaan saada selville, onko lääkkeessä oikeasti tehoa. Modernimpi esimerkki on verkkokaupan käyttöliittymän A/B-testaus, jossa satunnaisesti toisille asiakkaille nettisivulle näytetään punainen nappi ja toisille sininen nappi ja vertaillaan vaikuttaako napin väri sen klikkausten määrään.

Mikäli satunnaistetut kokeet eivät ole mahdollisia, voidaan yrittää metsästää luonnollisia kokeita. Esimerkiksi voidaan ottaa seurantaan henkilöt, jotka ovat juuri ja juuri päässeet läpi lääkiksen pääsykokeista ja vertailla tätä joukkoa niihin jotka jäivät niukasti ulos lääkiksestä. Voidaan olettaa että pienet erot pääsykokeen pistemäärissä jouhtuvat suurelta osin satunnaistekijöistä ja näin ollen on luotettavaa tehdä päätelmiä lääkiksen kausaalivaikutuksista loppuelämän onnellisuuteen.

Viimeisimpien vuosikymmenien aikana on erityisesti Judea Pearlin johdolla kehitetty kausaalimalleja, jotka auttavat tekemään kausaalipäätelmiä myös silloin kun käytössä havaittua dataa, mutta ei voida tehdä satunnaistettuja kokeita. Niissä aluksi pitää pystyä aiempiin tutkimuksiin perustuen rakentamaan graafi, josta näkee mitkä muuttujat vaikuttavat mielenkiinnon kohteina oleviin muuttujiin. Mikäli tärkeimmät näistä taustamuuttujista on mitattu, kausaalipäätelmät voivat olla mahdollisia.

Meidän kolmen muutttujan tapauksessa ilmiötä kuvaava graafi on esitelty kirjoituksen alussa. Tässä hyvin yksinkertaisessa maailmassa pystymme tutkimaan hukkumisten kausaalityhteyttä myyntiin. Kun laitamme sekä lämpötilan, että hukkumiset samaan regressiomalliin selittämään myyntiä, hukkumisella ei ole mitään selitysvoimaa, koska lämpötila on kaiken juurisyy. Näin ollen data näyttää, että ihmisiä on aivan turha alkaa hukuttamaan myynnin edistämiseksi.

Monimutkaisempien ilmiöiden tutkiminen kausaalimalleihin tukeutuen on itselläni vielä vaiheessa, joten ei kannata puhua tässä siitä sen enempää. Silti osa omaa analyysiprosessia on hahmotella graafiksi erilaisia potentiaalisia taustalla lymyileviä syy-seuraus-yhteyksiä, joita voi sitten asiaan paremmin vihkiytyneet haastaa. Mikäli mielenkiinto kausaalimalleihin heräsi, kannattaa aloittaa Judea Pearlin tietokirjasta ”The book of why”, josta Kimmo Pietiläinen on tehnyt myös suomenkielisen käännöksen: ”Miksi – syyn ja seurauksen uusi tiede”.

Ohjaileva analytiikka

Ohjaileva analytiikka on tässä lajittelussa laitettu viimeiseksi, koska pohjalla pitää olla alemman tason analytiikkaa päätöksenteon tueksi. Täältä huipulta kannattaa kuitenkin aina aloittaa pohtimalla, mitä halutaan tehdä. Mihin liittyviä päätöksiä analytiikalla halutaan parantaa? Esimerkkejä:

  • Halutaan kehittää jäätelönmyynnin logistiikkaa: miten paljon mitäkin makua pitäisi toimittaa kioskille, että asiakkaat saavat mitä haluavat, mutta jäätelöä ei tarvitsisi kohtuuttomia määriä pakastimessa varastoida. – > Ratkaisu: Päätöksenteon tueksi tarvitsemme ennakoivaa analytiikkaa, jolla arvioidaan kuinka paljon mitäkin makua menee ensi viikolla.
  • Halutaan lisätä jäätelön kysyntää. -> Ratkaisu: Diagnosoiva analytiikka. Johtopäätös on se, että korkeammat lämpötilat johtaisivat korkeampaan myyntiin. Mutta koska kaikki säiden hallitsemiseen kykenevät tahot ovat niin kallispalkkaisia, ei tällaista hanketta kannata toteuttaa. Laitetaan resurssit muun toiminnan kehittämiseen.

Kun pohjalla on riittävästi oppia analytiikan alemmilta tasoilta, ohjaileva analytiikka on pääasiassa erilaisia optimointialgoritmeja. Lisäksi on olemassa itseoppivia päätöksentekoalgoritmeja, jotka päivittävät omaa ymmärrystä aina päätöksestä tulleen palautteen perusteella.

Päätöksenteon optimointi on liian laaja aihe alkaa tässä syvemmin käsiteltäväksi, mutta se vaanii kaiken liiketoiminta-analytiikan taustalla. Ennen hosumista liian pitkälle datan kanssa, olisi hyvä ymmärtää mitä päätöksiä halutaan parantaa. Se mahdollistaa, että analytiikan alimmalta portaalta ponnistaessa edetään oikeaan suuntaan. Toisinaan matkalla opitaan jotain uutta, jonka vuoksi kurssia joudutaan kääntämään. Tämä tekee seikkailusta kuin seikkailusta entistä jännempää.

Lopputurinat

Dataan pohjautuvalla analytiikalla on useita eri tasoja ja niiden sisällä eri etenemispolkuja. Jotta varmistetaan datan penkomisen hyödyllisyys, aluksi pitäisi kirkastaa, mitkä päätöksentekoprosessit yrityksessä kaipaavat hiomista. Sitten valitaan sellainen polku, jota olemassa olevan datan pohjalta on mahdollista edetä. Lopulta päätöksenteko on kaksivaiheista: ensin opitaan, sitten päätetään.

Facebooktwitterredditpinterestlinkedinmail

Etäisyydet puolueista vaalikoneessa

Posted by :Statisticko On : 16.3.2019
0

Category: Algoritmit, Yhteiskunta

Tags:, , , ,

Helsingin Sanomien vaalikoneen ympärille syntyi pientä hässäkkää kun kansanedustaja Jyrki Kasvi huomasi, ettei hän nouse äänestäjän suosituslistalla ylimmäksi, vaikka äänestäjä vastaisi kaikkiin kysymyksiin täsmällisesti samoin kuin itse Kasvi.

Hesari lähti julkisesti avaamaan tätä ilmiötä ja selvisi että Jyrki Kasvi on Hesarin käyttämän algoritmin mielestä puolueista lähempänä Feministipuoluetta kuin edustamaansa Vihreää liittoa. Ehdokassuositukset taas jäljittelevät Suomen vaalikäytäntöä ja se antaa ensimmäisiksi suosituksiksi parhaat yksittäiset osumat ”lähimmästä” puolueesta ja vasta alempana puolueriippumattomasti lähimmät yksittäiset ehdokkaat. Kohun myötä Hesari tässä kirjoituksessa avasi käyttämänsä algoritmin toimintaa ja tarjosi dataa Uudenmaan vaalipiirin Feministipuolueen sekä Vihreän liiton ehdokkaiden vastauksista.

Seuraavassa esitellään muutamia vaihtoehtoisia tapoja ehdokkaiden sekä puolueiden läheisyyden mittaamiseen, käydään läpi Hesarin algoritmissa tehdyt valinnat ja katsotaan, kuinka Jyrki Kasville olisi käynyt vaihtoehtoisilla algoritmeilla.

Kahden yksittäisen ehdokkaan välinen etäisyys

Ehdokkat vastaavat Hesarin vaalikoneessa 30 kysymykseen, joten ehdokkaiden vastausten välistä etäisyyttä toisistaan mitataan 30-ulotteisessa avaruudessa. Tämä ei suinkaan ole yksiselitteinen tehtävä. Moniulotteisten etäisyyden mittaamiseen on olemassa useita eri mittareita. Näistä tunnetuimmat ovat Euklidinen-etäisyys (katso kaava) ja Manhattan-etäisyys (tai ”taksimetriikka”,katso kaava ja havainnollistus). Kun etäisyyttä mitataan Euklidisella etäisyydellä, peruskoulussa opitut geometrian lait pätevät. Datan analysointi ei kuitenkaan ole eksaktia matematiikkaa. Manhattan-etäisyydellä on se etu, ettei se ole niin herkkä reagoimaan yksittäisiin poikkeaviin havaintoihin.

Alla olevassa kuvaajassa on (kuviteltuna) esimerkkinä kahdelta ehdokkaalta vastaukset kahteen kysymykseen. Ensimmäinen ehdokas on antanut molempiin kysymykseen vastauksen 1 (”Täysin eri mieltä”). Toinen ehdokas on vastannut 1. kysymykseen 4 (”Jokseenkin samaa mieltä”) ja 2. kysymykseen 5 (”Täysin samaa mieltä”). Näiden kahden pisteen euklidinen etäisyys (punainen jana) on 5. Tämän voi varmistaa Pythagoraan lauseen avulla: $3^2 + 4^2 = 25 = 5^2 $. Eli kaikista janoista muodostuvan kolmion kateettien neliöiden summa on sama kuin hypotenuusan neliö. Geometrisessa tulkinnassa on kuitekin muistettava, että siinä täytyy olettaa vastausvaihtoehtojen välimatkat yhtä pitkiksi. Eli esimerkiksi ero ”Täysin eri mieltä” ja ”Jokseenkin erimieltä” välillä on sama kuin ”En osaa sanoa” ja ”Jokseenkin samaa mieltä” välillä.

Kahden pisteellä merkityn ehdokkaan välinen etäisyys eri mittareilla 2-ulotteisessa koordinaatistossa.

Manhattan-etäisyys taas määritellään mustien janojen määrittelemän ”kiertoreitin” pituutena. Tämä on 3 + 4 = 7. Hesari on päätynyt käyttämään vaalikoneen algoritmissaan tätä Manhattan-etäisyyttä kahden yksittäisen ehdokkaan välisen etäisyyden mittaamiseen.

Lopuksi vielä huomio, että kumpikaan esitellyistä etäisyysmittareista ei ota huomioon kysymysten välistä korrelaatiota. Mikäli usea kysymys liittyy samaan teemaan, tämä teema tulee korostumaan myös etäisyysmittarissa.

Etäisyys ryhmästä

Kun kahden ehdokkaan välinen etäisyysmittari on päätetty, pitää seuraavaksi päättää kuinka etäisyys puolueeseen mitataan. Hesari on laskenut etäisyyden jokaiseen puolueen ehdokkaaseen erikseen ja ottanut näistä keskiarvon. Toinen vaihtoehto olisi määritellä ensin puolueryhmän keskipiste 30-ulotteisessa avaruudessa ja laskea sitten etäisyys tähän yhteen pisteiseen. Ryhmän keskipisteenkin voi määritellä usealla eri tavalla, mutta pitäydytään nyt yksinkertaisimmassa: lasketaan kaikkien vastauksien keskiarvo ryhmän sisällä.

Ero usean yksittäisen ehdokkaan etäisyyden laskemisen ja keskipisteen laskemisen välillä on ainakin se, että yksittäisten etäisyyksien tapa rankaisee vaihtelusta puolueen sisällä. Otetaan esimerkiksi kaksi kahden hengen puoluetta. Puolueen 1 edustajat ovat molemmat vastanneet kysymykseen saman vastauksen 2. Puolueen 2 edustajista toinen on vastannut samaan kysymykseen 1 ja toinen 3. Mikäli Jyrki Kasvi olisi vastannut kysymykseen myös 2, etäisyyttä puolueeseen 1 kertyy 0 + 0 = 0. Etäisyyttä puolueeseen 2 taas kertyy 1 + 1 = 2. Molempien puolueiden keskiarvo on kuitenkin sama 2, joten keskiarvoon ei etäisyyttä kerry kumpaankaan puolueeseen lainkaan. Alla oleva taulukko vielä kokoaa yhteen em. esimerkin tulokset.

Puolue Ehdokas1Ehdokas2KAEtäisyys
yksilöihin		Etäisyys
keskiarvoon
Puolue122200
Puolue213220

Yllä olevan eron syntyminen kuitenkin vaatii, että Jyrki Kasvi on vastannut kysymykseen juuri 2. Muilla vastauksilla eroa mittaustapojen välillä ei tässä esimerkissä synny.

Hesari on päätynyt algoritmissaan mittaamaan etäisyyttä yksilöiden etäisyyksien kautta.

Vastausten vaihtelu puolueen sisällä

Kun Hesarin algoritmi mittaa etäisyyttää koko puolueesta tavalla, joka oletettavasti suosii sisäisesti saman mielistä ryhmää, on kiinnostavaa kuinka yhdenmielisiä Feministipuolueen ja Vihreiden jäsenet ovat. Alla olevassa kuvaajassa on lasketty yksittäisen ehdokkaiden vastaajien etäisyydet Manhattan-etäisyydellä. Mitä punaisempi väri, sitä lähempänä kyseiset ehdokkaat ovat toisiaan. Jokainen ehdokkaan etäisyys itsestään on luonnollisesti 0, mikä näkyy punaisena halkaisijana vasemmasta alanurkasta oikeaan ylänurkkaan.

Ehdokkaat 1-10 kuuluvat feministipuolueeseen ja ehdokkaat 11-40 Vihreisiin. Vasemmassa alanurkassa oleva yhtenäinen punainen neliö (tai oikeammin Tanskan lippu yhden yksittäisen sooloilijan ansiosta) kertoo, että Feministipuolueen jäsenet ovat hyvin yhdenmielisiä keskenään. Vihreiden joukossa nähdään sekä punaista että sinistä, mikä viestii vastauksien eroista puolueen sisällä.

Ehdokkaiden etäisyys toistaan Manhattan-etäisyydellä mitattuna. Punainen väri viittaa samankaltaisuuteen ja sininen eroihin vastauksissa.

Tulokset eri mittareilla

Lopuksi kiinnostavaa on, että olisiko tulokset erilaisia, mikäli algoritmin kehityksessä olisi tehty erilaisia valintoja. Nykyinen algoritmi antaa tulokseksi, että Jyrki Kasvin läheisyys Feministipuolueen kanssa on 79.3% ja Vihreiden kanssa 77.4%. Tein laskelmat vaihtoehtoisilla aiemmin tässä blogitekstissä esitetyillä menetelmillä hyödyntäen muilta osin Hesarin käyttämää ajatusta samankaltaisuuden laskemiseen. Tulokset ovat alla olevassa taulukossa. Alkuperäisen menetelmän tulokset ovat vasemmassa ylänurkassa.

Yksilöetäisyys ->
Ryhmämittari
ManhattanEuklidinen
Yksittäiset ehdokkaatFem 79.3%, Vih 77.4%Fem 65.6%, Vih 65.5%
RyhmäkeskiarvoFem 79.8%, Vih 78.9%Fem 67.6%, Vih 71.8%

Ennakko-oletukseni oli, että siirryttäessä mittaamaan ryhmän etäisyyttä ryhmäkeskiarvolla Vihreät menisivät Feministien ohi, koska puolueen sisäisistä eroista ei enää rankaistaisi. Olin väärässä. Todellisuudessa Vihreät hieman kirivät, mutta häviävät edelleen Feministipuolueelle 0.9 % -yksiköllä.

Siirtyminen alkuperäisestä algoritmista Euklidiseen etäisyyteen tasoittaisi tilannetta enemmän. Feministipuolue voittaisi enää olemattomalla 0.1% – yksikön erolla. Mikäli muutettaisiin molempia mittaustapoja, lopulta Vihreät menisivät Feministipuolueen ohi paalupaikalle prosentein 71.8% – 67.6%.

Kehitysehdotuksia

Tässä Jyrki Kasvin tapauksessa oli hyvin pienestä kiinni, tuleeko Feministipuolue vai Vihreät voittajaksi puolueen läheisyyden vertailussa. Itse olisin algoritmin kehityksessä todennäköisesti lähtenyt liikkeelle etäisyydestä puolueen keskipisteeseen ja ainakin pohtinut puolueiden erilaisten kokojen ja kysymysten välisten korrelaatioiden huomioimista jollain tavalla. Oma tämän hetken ymmärrys aiheesta ei kuitenkaan riitä painavasti kritisoimaan algoritmin kehittäjän valintoja käytetyissä etäisyysmittareissa.

Huoleni koskee lähinnä vaalikoneen tapaa suosia ronskisti voittaja-puoluetta esiin nostetuissa ehdokkaissa nyt kun voittajapuolueen voi tiukoissa kisoissa ratkaista valinnat algoritmin kehityksessä tai muut satunnaistekijät.

Kun itse tein Hesarin vaalikoneen, klikkasin kolmen ylimmäksi nousseen ehdokkaat lisätiedot uusiin välilehtiin ja siirryin tutkimaan niitä. Ainakin itseltäni on mennyt täysin ohi, että alempana on saattanut olla muista puolueista ehdokkaita, jotka osuvat vielä paremmin omiin valintoihin. Ensimmäinen kehityskohde voisikin olla tämän asian selkeämpi viestiminen kiireiselle käyttäjälle.

Yleisemmällä tasolla tämä esimerkki havainnollistaa, kuinka todellisessa maailmassa, eksaktin matematiikan ulkopuolella, algoritmien kehitys on aina jossain määrin taidetta ja kehittäjän tekemät valinnat vaikuttavat jossain määrin tuloksiin. Tässäkin tapauksessa voittaja olisi ollut Vihreät, mikäli olisi käytetty ryhmäkeskiarvoja ja Euklidista etäisyyttä.

Mitä enemmän algoritmilla on vaikutusta ihmisiin, sitä tärkeämpää on niitä julkistaa ja altistaa kritiikille sekä kehotusehdotuksille. Tästä ryhdikäs hatun nosto Hesarille.

Facebooktwitterredditpinterestlinkedinmail

Itseään toistavat algoritmit

Posted by :Statisticko On : 28.2.2018
0

Category: Algoritmit, Asuntokaupat

Tags:, , , ,

Ikääntymisen myötä olen tullut koko ajan laiskemmaksi etsimällä etsimään uusia bändejä kuuneltavaksi. Eräs syy, miksi tykkään Spotifyn musiikkipalvelusta on heidän ”Viikon suositukset” listansa.  Tälle listalle valikoituu biisejä, joista saattaisin heidän algoritmiensa mukaan tykätä viime aikojen musiikinkuuntelun perusteella. Tämä on erittäin kätevä tapa löytää uusia itselleen iskeviä bändejä. Tälläkin hetkellä luukutan lupaavan kuuloista metalliorkesteria ”Fight the Fight”, mihin en ihan heti olisi törmännyt ilman Spotifya.

Dataa omista ennusteista

”Viikon suositukset” -listaa tulee kuunneltua usein taustamusiikkina ilman, että skippailisin yli biisejä, vaikka ne eivät maistu eli ovat ns. vikasuosituksia. En tiedä, käsitteleekö Spotifyn algoritmi loppuunkuunneltuja biisejä todellisina musiikkimakuani kuvaavana havaintona, vaikka ne tulisi soittoon sen oman suosituksen kautta. Tämän takia olen hieman vainoharhaisesti pitänyt taukoja huonosti osuneiden viikkojen jälkeen ja kuunnellut vain itse valitsemaa musiikkia, ettei algoritmi vaan alkaisi opettaman itseään omilla virheillään.

Mitä haittaa siitä sitten oikeasti olisi, mikäli joku algoritmi ei tunnista itsensä syöttämiä havaintoja? Tätä lähdetään nyt selvittämään asuntohinta-aineiston avulla.

Hinta-arviot algoritmilla

Siinä ei varmaan ole mitään yllättävää että iso osa pörssissä tehtävästä kaupankäynnistä tulee automaattisesti hinnoittelua suorittavien algoritmien toimesta. Sama ajatus asuntokaupassa tuntuu hieman etäisemmältä, mutta leikitellään vähän ajatuksella.

Olen ollut kehittämässä muutama vuosi sitten ASLA -asuntolaskuria, joka pyrkii antamaan kerrostaloasunnoille markkinahinta-arvioita julkisen datan perusteella. Asuntojen hinnat määräytyvät lukuisten ihmisten mieltymysten ja preferenssien perusteella. ASLAn taustalla oleva algoritmi pyrkii käytettävissä olevan datan avulla muuttamaan kaupankävijöiden keskimääräisiä mieltymyksiä matemaattisiksi kaavoiksi. Mitä tapahtuisi, jos osassa kaupoista normaali tinkimisprosessi jäisi pois ja sekä myyjä että ostaja luottavat ASLAn arvioon tehden kauppansa mukisematta kyseisillä arvioilla?

Seuraavassa olen simuloinut tällaista prosessia niin että vuodesta 2014 alkaen osassa todellisista asuntokaupoista hinta korvataankin ASLAn käyttämän algoritmin arviolla (korvattavat valitaan satunnaisesti) ja joka vuoden päätteeksi algoritmi kouluttaa itseään lisää uudella kertyneellä datalla. Aineistona käytetään Helsingin yksiöitä ja otoskoko-ongelmien välttämiseksi mukana on vain kymmenen kaupankäyntimäärältään suosituinta postinumeroaluetta.

Kuvaajassa olevat viivat kuvaavat kolmea eri virheprosenttia vuosina 2014-2017:

  • Ristiinvalidointi (punainen): Etukäteisarvio algoritmin hinta-arvion ja todellisten hintojen keskimääräisestä prosentuaalisesta erosta. Ristiinvalidoinnin ideasta lisää tällä videolla.
  • Todellinen (vihreä): Algoritmin hinta-arvioiden ja todellisten, ihmisten määrittelemien hintojen, keskimääräinen prosentuaalinen ero
  • Näennäinen (sininen): Hinta-arvioiden ja havaittujen hintojen keskimääräinen prosentuaalinen ero, kun mukana on myös algoritmin avulla määritellyt kauppahinnat

Ensimmäisessä kuvaajassa (ylhäällä) kukaan kaupankävijä ei käytä ASLAa vaan kaikki myyntihinnat ovat aitoja ihmisten preferensseihin perustuvia hintoja. Sekä ennalta arvioidut että todellisuudessa kohdatut virheprosentit pyörivät lähellä toisiaan 8% – 9% välimaastossa.

Seuraavissa kuvissa aina tietyn vuoden vuoden oikeita kauppahintoja korvataan ASLAn ennusteilla. Ensin satunnaisesti 25%, sitten puolet, sitten 75% ja viimeisessä kuvaajassa kaikki. Huomataan että ajan kuluessa algoritmin itsevarmuus kasvaa, eli punainen ristiinvalidointiin perustuvat virhearvioennusteet pienenevät. Mutta todellinen kyky arvioida ihmisten preferenssejä kuitenkin laskee, koska vihreä käyrä kasvaa kohti suurempia lukemia. Efekti on sitä selvempi, mitä isompi osuus kauppahinnoista tulee algoritmin perusteella. Ääritapauksessa oikealla, missä kaikki kauppahinnat tulevat suoraan algoritmista, havaitut ennustevirheet ovat nollassa (sininen käyrä), mutta kyky arvioida ihmisten preferenssejä (vihreä käyrä) on aivan jotain muuta.

Omat ennusteet eivät ole aitoja havaintoja

Kun asuntoja hinnoitellaan suoraan algoritmin perusteella, alkaa algoritmin satunnaiset virheet toistumaan ja erityisesti se ei osaa sopeutua ajan tuomiin muutoksiin. Esimerkiksi algoritmi ei ymmärrä, että asuntojen hintoihin kohdistuu laskupainetta, mikäli korot tai kiinteistöverot nousevat äkillisesti. Nyt jos näitä muutoksia ei korjata aidolla uudella datalla, algoritmi alkaa irtaantumaan todellisista ihmisten preferensseistä.

ASLAa ei ole missään nimessä tarkoitettu automaattiseksi hinnoittelijaksi korvaamaan täysin kiinteistövälittäjiä vaan kauppaa käyvän ihmis-olion apuvälineeksi. Se antaa tukea erityisesti kokemattomalle kaupankävijälle uudella paikkakunnalla, mutta jättää huomioimatta monia tärkeitä asioita, kuten tehdyt taloyhtiöremontit ja tonttien omistusoikeudet. Algoritmi tehostaa ja tarkentaa ihmisen työtä tiivistämällä kaiken datassa olevan tiedon sekunnissa ilman että tarvitsee manuaalisesti (silmin selaimella tai Exceliä yötä myöden hakkaamalla) yrittää datasta ottaa tolkkua. Ihminen voi käyttää omat resurssinsa siihen, mitä kone ei osaa eli tässä tapauksessa esimerkiksi arvioida tulevia remontteja ja havainnoida esteettisiä kokemuksia paikan päällä.

Itse luotujen havaintojen siivoaminen

Palaten alkuperäiseen pohdintaan algoritmien omien havaintojen käyttämisessä sen opettamisessa, meillä on kädessä ongelma. Kuten asuntohintojen tapauksessa huomattiin, sitä mukaa kun itse luotua dataa kertyy lisää, algoritmin ”itseluottamus” kasvaa samalla kun todellinen performanssi heikkenee.

Spotifyn algoritmin on mahdollista (ja omasta vainoharhaisuudesta huolimatta näin mahdollisesti tekeekin) kehäpäätelmät välttää, koska jossain heidän tietokannassaan luulisi olevan tieto, valitsiko käyttäjä jonkin kappaleen soimaan omatoimisesti vai tuliko se suosituksen kautta automaattisesti. Jälkimmäiset tulee putsata pois datasta, jolla algoritmia jatkokoulutetaan. Asuntohinta-esimerkki on kinkkisempi, koska emme tiedä, onko joku tietty kaupankävijä käyttänyt algoritmia vai ei.

Mitä tulee ASLAn tulevaisuuteen, herää kysymys: ”Kannattaako laskurin näkyvyyttä yrittää lisätä, jos riskinä on, että siitä tulee sitä epätarkempi, mitä useampi sitä käyttää?” Kaupallinen käyttökin on kielletty taustalla käytettävän datan käyttöehtojen takia.

Statistickon steesit:

  • Algoritmin kouluttaminen sen itse luomalla datalla on kehäpäätelmä
  • Ajan myötä taustaolosuhteiden muuttuessa algoritmit tuppaavan irtaantumaan todellisuudesta, ellei niitä kouluteta uusilla, aidoilla havainnoilla
  • Omien ennusteiden käyttäminen opetusdatana vielä huonontaa tilannetta antamalla valheellisen illuusion tarkentuvista ennusteista

Facebooktwitterredditpinterestlinkedinmail

Datan määrä ei korvaa ymmärrystä

Posted by :Statisticko On : 31.10.2017
0

Category: Algoritmit, Ennustaminen

Kun valtamedioista lukee jotain big dataan tai tekoälyyn liittyvää, mielikuvaksi datan ennakoivasta analyysistä voi usein jäädä jotain seuraavaa: ”pitää vaan olla massiivinen läjä dataa niin neuroverkot ja muut koneoppimisalgoritmit kyllä taikovat automaagisesti suurta viisautta”. Tähän väliin ajattelin tuoda nyt esiin vähän toista puolta sopan aineksista. Jossain kohtaa nimittäin edelleen tarvitaan tutkittavan ilmiön ymmärtämistä dataa pursuavista tietokannoista ja fiksuista koneoppimisalgoritmeista huolimatta.

Kurssisuoritusten ennustaminen

Viestin havainnollistamista auttakoon meitä kuvitteellinen tarina kahdesta Data Scientististä, Laiska-Latesta ja Nysvä-Niilosta. Molemmille on annettu tehtäväksi kehittää algoritmi, joka ennustaa etukäteen ketkä pääsevät läpi erään opiston valinnaisen kurssin kokeesta. Koe on vaikea ja se on pisteytetty niin, että vain puolet yrittäjistä pääsevät läpi. Opisto kouluttaa naisvaltaiselle alalle ja opiskelijoiden sukupuolijakauma on vuodesta toiseen suurin piirtein 80% naisia ja 20% miehiä.

Laiska-Late löytää opiston nettisivuilta kurssilaisista valmista dataa menneiltä vuosilta seuraavista tiedoista:

  • kokeen läpäiseminen
  • kurssin aikana kerätyt harjoituspisteet
  • sairauspoissaolot oppitunneilta

Tietosuojasyistä oppilaiden nimiä tai muita taustatietoja ei ole kuitenkaan tallennettu. Kaikki henkilötiedot on vain korvattu ID-numerolla. Havaintoja on kuitenkin iso  määrä tähän tarkoitukseen.

Erilaisten mallien kokeilun ja validointien jälkeen Latelle jää vielä 5000 havaintoa lopulliseen parametrien optimointiin. Hän päätyy logistiseen regressiomalliin, jossa kokeen läpäisyä (kyllä/ei) ennustaa kurssin aikana kerätyt harjoituspisteet. Sairauspoissaolo-tiedosta ei ollut hyötyä ennustamisessa.

Harjoituspisteiden ja kokeen läpäisemisen riippuvuussuhdetta kuvaa oheinen viiksilaatikko – kuvaaja, mistä näkyy että kokeen läpäisseillä on keskimäärin VÄHEMMÄN kerättyjä harjoituspisteitä. Late ei tähän takerru, koska data puhuu  tämän puolesta ja ero on selvästi tilastollisesti merkitsevää. Tähän riippuvuussuhteeseen perustuu hänen ennustusmallinsa ja siinä on kaikki mitä näillä tiedoilla on tehtävissä.

Nysvä-Niilo lähestyy ongelmaa hieman eri polkua. Hän aloittaa tutkimalla tarkemmin, mitä kurssi ja erityisesti loppukoe pitää sisällään ja jalkautuu opistolle jututtamaan opiskelijoita. Tässä alkukartoituksessa selviää ensinnäkin, että koe sisältää myös fyysistä nopeutta ja voimaa sisältäviä osuuksia. Näin ollen voisi veikata, että opiston miesopiskelijoilla olisi etulyöntiasema naisiin nähden. Toinen keskusteluissa esiin tullut huomio on, että naiset vaikuttavat miehiä tunnollisemmilta tekemään harjoitustehtäviä. Niilokin tietää nettisivuilla tarjolla olevasta datasetistä, mutta koska näkee sukupuolen niin tärkeänä tekijänä ilmiön kokonaisuutta hän päättää alkaa nysväämään ja keräämään seurantatutkimuksella dataa opiskelijoiden harjoituspisteitä, koemenestyksestä ja sukupuolesta. Rajallisten resurssien ja aikataulun vuoksi hän saa kasaan vain 200 havaintoa. Nämä havainnot kuitenkin tukevat Niilon alustavaa hypoteesia siitä, että sukupuoli selittää sekä koetulosta, että harjoituspistemääriä. Oheinen graafi kuvaa Nysvä-Niilon näkemystä oleellisista ilmiöön liittyvistä oleellisista riippuvuussuhteista.

Niilo käyttää myös ennustealgoritminaan logistista regressiota, mutta Laten malliin lisäyksenä on sukupuoli toisena selittäjänä ja dataa vain 200 havaintoa.

Niilon datalla piirretään harjoituspisteiden ja läpäisyjen yhteyttä kuvaava graafi, mutta sukupuolittain eriteltyinä niin huomataan, että sukupuoliryhmissä kokeessa hyväksytyt ovat tehneet keskimäärin hieman ENEMMÄN harjoituksia. Tämähän vaikuttaa ristiriitaiselta Laiska-Laten tulokseen verrattuna. Onko se vain sattumaa, koska Nysvä-Niilon aineisto on niin pieni? Sekin voisi olla mahdollista, mutta tässä tapauksessa ei (tiedän, koska olen itse simuloinut aineiston). Harjoituspisteet ennustavat kyllä parempaa menestystä kokeessa, mutta koska fyysisten elementtien takia kokeessa alakynnessä olevat naiset ovat paljon tunnollisempia harjoitusten tekijöitä, näyttäytyy riippuvuussuhde päinvastaisena silloin kun sukupuolta ei huomioida. Tällaista kolmen muuttujan riippuvuussuhdetta kutsutaan Simpsonin paradoksiksi (linkki Wikipedian artikkeliin).

Kuinkas sitten käykään Laten ja Niilon ennusteille tositoimissa? Meneekö Laten ennusteet täysin päin mäntyä? Ei välttämättä. Vanha viisaus (en muista kenen) sanoo, että ”Vaikkei joku korrelaatio johtuisi kausaliteetista, voi siitä silti olla hyötyä ennustamisessa”. Seuraavana vuonna kurssille osallistuu 500 henkilöä ja näille ennustetarkkuudet ovat seuraavat:

Laiska – Late: 65%

Nysvääjä – Niilo: 68%

Unelmatilanteessa meillä olisi paljon sekä ymmärrystä että dataa. Nyt molemmilla on vain toinen puoli kunnossa. Sen minkä Niilon ennusteet voittavat hyödyllisen sukupuoli-muuttujan on mittaamisella, hän häviää siinä, että vain 200 hengen otoksella hänen mallinsa parametreissa on epätarkkuutta. Molemmat kuitenkin pärjäävät selvästi kolikonheittoa paremmin, joten jotain lisäarvoa he ovat tuoneet.

Iso uutinen tulee kuitenkin vasta seuraavana vuonna. Voimaan tulee uusi asetus, jonka johdosta tasa-arvon nimissä opiston on otettava sisään yhtä paljon miehiä ja naisia. Tämän uudistuksen jälkeisellä 500 kurssilaisen ennusteilla ennustealgoritmien erot repeävät.

Laiska – Late: 58%

Nysvääjä – Niilo: 67%

Algoritmeissa oli piilotettuna oletus ”kaikki muut ilmiöön vaikuttavat asiat pysyvät samankaltaisena”. Nyt sukupuolijakauman muutos rikkoo tämän oletuksen Laten algoritmin kohdalla ja tältä algoritmilta lähti matto alta. Se voittaa lantinheiton enää vaivoin. Niilon syy-seuraus -suhteita paremmin ymmärtävässä mallissa sukupuoli oli huomioitu, joten se ei uudesta asetuksesta juuri hetkahda.

Mitä pitää vähintään tietää?

Edellä kerrottu esimerkki oli tarkoitushakuinen ja äärimmäistapaus. Toivottavasti se kuitenkin havainnollisti vaaranpaikkoja silloin kun emme ymmärrä havaintojen muodostumisen taustaprosessia. Sen lisäksi, että algoritmin kehittäjä hehkuttaa ennusteiden tarkkuutta käytössä olevalla datalla, hänen pitäisi pystyä vastaamaan myös ainakin seuraaviin kysymyksiin:

  • Missä olosuhteissa algoritmia on turvallista soveltaa ja missä ei?
  • Osaako algoritmi opettaa itseään ja milloin algoritmi pitää kouluttaa täysin uusiksi?

Hyödyllisiä työkaluja

Tarkoitukseni ei ole kuitenkaan yleisesti mollata suurten datamassoja ja niiden päälle rakennettujen koneoppimisalgoritmien hyötyjä. Nämä nimittäin mahdollistavat todella siistejä työkaluja kuten vaikka eläinlajin tunnistamista kuvasta tai kielen koneellista ymmärrystä. Molemmat ilmiöt sopivat hyvin ”black-box” algoritmien (soveltaja ei ymmärrä tarkalleen mihin algoritmi ennusteensa perustaa) maailmaan, koska ne ovat hyvin stabiileja. Vaikka kieli pikkuhiljaa kehittyy ja joidenkin sanojen merkitys vuosikymmenten saatossa muuttuu, on vaikea kuvitella miksei tänään koulutettu puheentunnistaja voisi toimia lähes yhtä hyvin myös vuoden päästä. Kissan ja koiran piirteiden muuttumista joutuu odottamaan vieläkin kauemmin.

Weapons of math destruction

Suurimmat vaarat pelkkään isoon datamassaan ja sen korrelaatioihin luottavaan ”black-box”-algoritmiin tulevat esille, kun se koskee ihmisen luokittelua tai arvottamista. Silloin meillä on käsillä kohonnut riski, että olemme luomassa algoritmia, jota matemaatikko Cathy O’Neil kutsuu termillä ”Weapon of math destruction” (TED-talk aiheesta). Tällaiset tuho-algoritmit ovat rasistisia tavalla, jota algoritmin käyttäjät eivät ymmärrä. Esimerkiksi USA:laisessa pankissa voitaisiin arvioida asiakasehdokkaiden luottokelpoisuutta automaattisesti heidän lainahakemustensa perusteella. Algoritmi mm. hyödyntää isossa datamassassa havaittua korrelaatiota hakemusten kirjoitusvirheiden määrän ja maksuhäiriömerkintöjen välillä. Nyt lainaa voisi olla hakemassa suomalainen insinööri, joka on 23-vuotiaana muuttanut USA:han suorittamaan jatko-opintoja. Hän on erittäin tunnollisesti aina hoitanut velvoitteensa, mutta joutuu syrjityksi asuntolainamarkkinoilla vain koska hän tekee maahanmuuttajataustaisena keskimääräistä amerikkalaista enemmän kielioppivirheitä.

Kielioppivirheet tuskin kuitenkaan ovat aito syy maksuhäiriöille vaan näiden takaa löytyy yhteisiä taustatekijöitä. Kun kaikkia aitoja selittäjiä taustalla ei pystytä mittaamaan, auttavat näennäisetkin korrelaatiot parantamaan ennustetarkkuutta isossa joukossa. Harmi vaan niille jotka joutuvat aiheetta kärsimään siitä, että juuri tähän näennäiskorrelaatioon sattui algoritmi tarraamaan.

Loppusanat

Ennustusalgoritmien rakentamisessa toivottavaa olisi olla hyvä tieteellinen ymmärrys ilmiöstä ja paljon tarkasti mitattua dataa kaikista oleellisista muuttujista. Käytännössä tutkittavat ilmiöt tuppaavat olemaan niin monimutkaisia, ettei kaikkien oleellisten muuttujien mittaaminen ole aina mahdollista. Suurikaan havaintojen määrä ei pysty täysin korvaamaan puutteita muuttujissa, mutta ajassa stabiileihin ilmiöihin voi silti rakentaa korrelaatioihin perustuvia hyödyllisiä algoritmeja. Nämä algoritmit ovat kuitenkin vain työkaluja, joiden ohjaksissa olevien pitää ymmärtää työkalunsa rajoitteet.

Ymmärrykseen pyrkivän analytiikan nostaminen jalustalle voi olla osaltani vääristynyttä hehkutusta, koska oma osaamiseni ja mielenkiintoni on sinne päin kallellaan. On siitä kuitenkin puhuneet muutkin Data Scientistit, vaikkakin lähinnä marginaalisimmissa medioissa. Tässä blogikirjoituksessa Manish Tripathi maalailee datan analysoimisen tulevaisuutta ja viesti tiivistettynä kuuluu: koneoppimisalgoritmin koulutus tulee automatisoitumaan ja pelkästään sen parissa työskentelevät Data Scientistit alkavat kohtapuoliin menettämään työpaikkojaan. Sen sijaan syy-seuraus-suhteita ymmärtävistä Data Scientisteista tulee olemaan pulaa.

Ja loppuksi vielä lainaus Hilary Masonilta tästä podcastista: ”You cannot do AI without machine learning, you cannot do machine learning without data science and you cannot do data science without analytics”Facebooktwitterredditpinterestlinkedinmail