Helsingin Sanomien vaalikoneen ympärille syntyi pientä hässäkkää kun kansanedustaja Jyrki Kasvi huomasi, ettei hän nouse äänestäjän suosituslistalla ylimmäksi, vaikka äänestäjä vastaisi kaikkiin kysymyksiin täsmällisesti samoin kuin itse Kasvi.
Hesari lähti julkisesti avaamaan tätä ilmiötä ja selvisi että Jyrki Kasvi on Hesarin käyttämän algoritmin mielestä puolueista lähempänä Feministipuoluetta kuin edustamaansa Vihreää liittoa. Ehdokassuositukset taas jäljittelevät Suomen vaalikäytäntöä ja se antaa ensimmäisiksi suosituksiksi parhaat yksittäiset osumat ”lähimmästä” puolueesta ja vasta alempana puolueriippumattomasti lähimmät yksittäiset ehdokkaat. Kohun myötä Hesari tässä kirjoituksessa avasi käyttämänsä algoritmin toimintaa ja tarjosi dataa Uudenmaan vaalipiirin Feministipuolueen sekä Vihreän liiton ehdokkaiden vastauksista.
Seuraavassa esitellään muutamia vaihtoehtoisia tapoja ehdokkaiden sekä puolueiden läheisyyden mittaamiseen, käydään läpi Hesarin algoritmissa tehdyt valinnat ja katsotaan, kuinka Jyrki Kasville olisi käynyt vaihtoehtoisilla algoritmeilla.
Kahden yksittäisen ehdokkaan välinen etäisyys
Ehdokkat vastaavat Hesarin vaalikoneessa 30 kysymykseen, joten ehdokkaiden vastausten välistä etäisyyttä toisistaan mitataan 30-ulotteisessa avaruudessa. Tämä ei suinkaan ole yksiselitteinen tehtävä. Moniulotteisten etäisyyden mittaamiseen on olemassa useita eri mittareita. Näistä tunnetuimmat ovat Euklidinen-etäisyys (katso kaava) ja Manhattan-etäisyys (tai ”taksimetriikka”,katso kaava ja havainnollistus). Kun etäisyyttä mitataan Euklidisella etäisyydellä, peruskoulussa opitut geometrian lait pätevät. Datan analysointi ei kuitenkaan ole eksaktia matematiikkaa. Manhattan-etäisyydellä on se etu, ettei se ole niin herkkä reagoimaan yksittäisiin poikkeaviin havaintoihin.
Alla olevassa kuvaajassa on (kuviteltuna) esimerkkinä kahdelta ehdokkaalta vastaukset kahteen kysymykseen. Ensimmäinen ehdokas on antanut molempiin kysymykseen vastauksen 1 (”Täysin eri mieltä”). Toinen ehdokas on vastannut 1. kysymykseen 4 (”Jokseenkin samaa mieltä”) ja 2. kysymykseen 5 (”Täysin samaa mieltä”). Näiden kahden pisteen euklidinen etäisyys (punainen jana) on 5. Tämän voi varmistaa Pythagoraan lauseen avulla: ![]() . Eli kaikista janoista muodostuvan kolmion kateettien neliöiden summa on sama kuin hypotenuusan neliö. Geometrisessa tulkinnassa on kuitekin muistettava, että siinä täytyy olettaa vastausvaihtoehtojen välimatkat yhtä pitkiksi. Eli esimerkiksi ero ”Täysin eri mieltä” ja ”Jokseenkin erimieltä” välillä on sama kuin ”En osaa sanoa” ja ”Jokseenkin samaa mieltä” välillä.
. Eli kaikista janoista muodostuvan kolmion kateettien neliöiden summa on sama kuin hypotenuusan neliö. Geometrisessa tulkinnassa on kuitekin muistettava, että siinä täytyy olettaa vastausvaihtoehtojen välimatkat yhtä pitkiksi. Eli esimerkiksi ero ”Täysin eri mieltä” ja ”Jokseenkin erimieltä” välillä on sama kuin ”En osaa sanoa” ja ”Jokseenkin samaa mieltä” välillä.
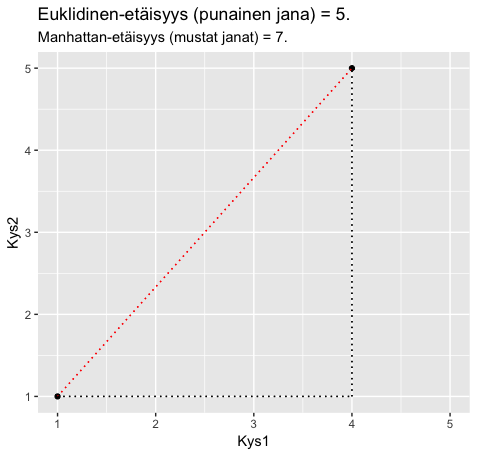
Manhattan-etäisyys taas määritellään mustien janojen määrittelemän ”kiertoreitin” pituutena. Tämä on 3 + 4 = 7. Hesari on päätynyt käyttämään vaalikoneen algoritmissaan tätä Manhattan-etäisyyttä kahden yksittäisen ehdokkaan välisen etäisyyden mittaamiseen.
Lopuksi vielä huomio, että kumpikaan esitellyistä etäisyysmittareista ei ota huomioon kysymysten välistä korrelaatiota. Mikäli usea kysymys liittyy samaan teemaan, tämä teema tulee korostumaan myös etäisyysmittarissa.
Etäisyys ryhmästä
Kun kahden ehdokkaan välinen etäisyysmittari on päätetty, pitää seuraavaksi päättää kuinka etäisyys puolueeseen mitataan. Hesari on laskenut etäisyyden jokaiseen puolueen ehdokkaaseen erikseen ja ottanut näistä keskiarvon. Toinen vaihtoehto olisi määritellä ensin puolueryhmän keskipiste 30-ulotteisessa avaruudessa ja laskea sitten etäisyys tähän yhteen pisteiseen. Ryhmän keskipisteenkin voi määritellä usealla eri tavalla, mutta pitäydytään nyt yksinkertaisimmassa: lasketaan kaikkien vastauksien keskiarvo ryhmän sisällä.
Ero usean yksittäisen ehdokkaan etäisyyden laskemisen ja keskipisteen laskemisen välillä on ainakin se, että yksittäisten etäisyyksien tapa rankaisee vaihtelusta puolueen sisällä. Otetaan esimerkiksi kaksi kahden hengen puoluetta. Puolueen 1 edustajat ovat molemmat vastanneet kysymykseen saman vastauksen 2. Puolueen 2 edustajista toinen on vastannut samaan kysymykseen 1 ja toinen 3. Mikäli Jyrki Kasvi olisi vastannut kysymykseen myös 2, etäisyyttä puolueeseen 1 kertyy 0 + 0 = 0. Etäisyyttä puolueeseen 2 taas kertyy 1 + 1 = 2. Molempien puolueiden keskiarvo on kuitenkin sama 2, joten keskiarvoon ei etäisyyttä kerry kumpaankaan puolueeseen lainkaan. Alla oleva taulukko vielä kokoaa yhteen em. esimerkin tulokset.
| Puolue | Ehdokas1 | Ehdokas2 | KA | Etäisyys yksilöihin | Etäisyys keskiarvoon |
|---|---|---|---|---|---|
| Puolue1 | 2 | 2 | 2 | 0 | 0 |
| Puolue2 | 1 | 3 | 2 | 2 | 0 |
Yllä olevan eron syntyminen kuitenkin vaatii, että Jyrki Kasvi on vastannut kysymykseen juuri 2. Muilla vastauksilla eroa mittaustapojen välillä ei tässä esimerkissä synny.
Hesari on päätynyt algoritmissaan mittaamaan etäisyyttä yksilöiden etäisyyksien kautta.
Vastausten vaihtelu puolueen sisällä
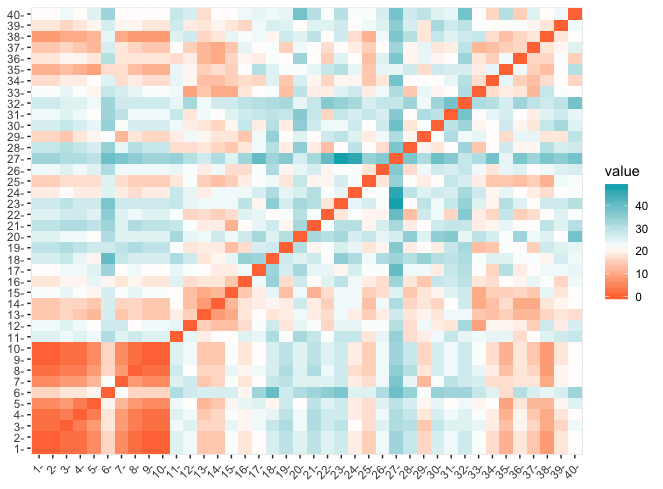
Kun Hesarin algoritmi mittaa etäisyyttää koko puolueesta tavalla, joka oletettavasti suosii sisäisesti saman mielistä ryhmää, on kiinnostavaa kuinka yhdenmielisiä Feministipuolueen ja Vihreiden jäsenet ovat. Alla olevassa kuvaajassa on lasketty yksittäisen ehdokkaiden vastaajien etäisyydet Manhattan-etäisyydellä. Mitä punaisempi väri, sitä lähempänä kyseiset ehdokkaat ovat toisiaan. Jokainen ehdokkaan etäisyys itsestään on luonnollisesti 0, mikä näkyy punaisena halkaisijana vasemmasta alanurkasta oikeaan ylänurkkaan.
Ehdokkaat 1-10 kuuluvat feministipuolueeseen ja ehdokkaat 11-40 Vihreisiin. Vasemmassa alanurkassa oleva yhtenäinen punainen neliö (tai oikeammin Tanskan lippu yhden yksittäisen sooloilijan ansiosta) kertoo, että Feministipuolueen jäsenet ovat hyvin yhdenmielisiä keskenään. Vihreiden joukossa nähdään sekä punaista että sinistä, mikä viestii vastauksien eroista puolueen sisällä.
Tulokset eri mittareilla
Lopuksi kiinnostavaa on, että olisiko tulokset erilaisia, mikäli algoritmin kehityksessä olisi tehty erilaisia valintoja. Nykyinen algoritmi antaa tulokseksi, että Jyrki Kasvin läheisyys Feministipuolueen kanssa on 79.3% ja Vihreiden kanssa 77.4%. Tein laskelmat vaihtoehtoisilla aiemmin tässä blogitekstissä esitetyillä menetelmillä hyödyntäen muilta osin Hesarin käyttämää ajatusta samankaltaisuuden laskemiseen. Tulokset ovat alla olevassa taulukossa. Alkuperäisen menetelmän tulokset ovat vasemmassa ylänurkassa.
| Yksilöetäisyys -> Ryhmämittari | Manhattan | Euklidinen |
|---|---|---|
| Yksittäiset ehdokkaat | Fem 79.3%, Vih 77.4% | Fem 65.6%, Vih 65.5% |
| Ryhmäkeskiarvo | Fem 79.8%, Vih 78.9% | Fem 67.6%, Vih 71.8% |
Ennakko-oletukseni oli, että siirryttäessä mittaamaan ryhmän etäisyyttä ryhmäkeskiarvolla Vihreät menisivät Feministien ohi, koska puolueen sisäisistä eroista ei enää rankaistaisi. Olin väärässä. Todellisuudessa Vihreät hieman kirivät, mutta häviävät edelleen Feministipuolueelle 0.9 % -yksiköllä.
Siirtyminen alkuperäisestä algoritmista Euklidiseen etäisyyteen tasoittaisi tilannetta enemmän. Feministipuolue voittaisi enää olemattomalla 0.1% – yksikön erolla. Mikäli muutettaisiin molempia mittaustapoja, lopulta Vihreät menisivät Feministipuolueen ohi paalupaikalle prosentein 71.8% – 67.6%.
Kehitysehdotuksia
Tässä Jyrki Kasvin tapauksessa oli hyvin pienestä kiinni, tuleeko Feministipuolue vai Vihreät voittajaksi puolueen läheisyyden vertailussa. Itse olisin algoritmin kehityksessä todennäköisesti lähtenyt liikkeelle etäisyydestä puolueen keskipisteeseen ja ainakin pohtinut puolueiden erilaisten kokojen ja kysymysten välisten korrelaatioiden huomioimista jollain tavalla. Oma tämän hetken ymmärrys aiheesta ei kuitenkaan riitä painavasti kritisoimaan algoritmin kehittäjän valintoja käytetyissä etäisyysmittareissa.
Huoleni koskee lähinnä vaalikoneen tapaa suosia ronskisti voittaja-puoluetta esiin nostetuissa ehdokkaissa nyt kun voittajapuolueen voi tiukoissa kisoissa ratkaista valinnat algoritmin kehityksessä tai muut satunnaistekijät.
Kun itse tein Hesarin vaalikoneen, klikkasin kolmen ylimmäksi nousseen ehdokkaat lisätiedot uusiin välilehtiin ja siirryin tutkimaan niitä. Ainakin itseltäni on mennyt täysin ohi, että alempana on saattanut olla muista puolueista ehdokkaita, jotka osuvat vielä paremmin omiin valintoihin. Ensimmäinen kehityskohde voisikin olla tämän asian selkeämpi viestiminen kiireiselle käyttäjälle.
Yleisemmällä tasolla tämä esimerkki havainnollistaa, kuinka todellisessa maailmassa, eksaktin matematiikan ulkopuolella, algoritmien kehitys on aina jossain määrin taidetta ja kehittäjän tekemät valinnat vaikuttavat jossain määrin tuloksiin. Tässäkin tapauksessa voittaja olisi ollut Vihreät, mikäli olisi käytetty ryhmäkeskiarvoja ja Euklidista etäisyyttä.
Mitä enemmän algoritmilla on vaikutusta ihmisiin, sitä tärkeämpää on niitä julkistaa ja altistaa kritiikille sekä kehotusehdotuksille. Tästä ryhdikäs hatun nosto Hesarille.
