”Kaunis mieli”-elokuva on tositapahtumiin perustuva tarina peliteorian merkittävästä kehittäjästä; Nobel-palkitusta John Nashista. Ainakin elokuvan mukaan ensimmäinen peliteorian sovellus oli parinvalintatilanne opiskelijakemuissa: muiden miesten pörrätessä saman kauneimman naisen ympärillä, John laski maksimoivansa omat odotuksensa illan iloille satsaamalla huomionsa toiseksi kauneimpaan. Parhaiten nykymatematiikassa hänet tunnetaan Nashin tasapainoteoriasta. Kyse on kilpailutilanteesta, jossa kaikki osapuolet pelavaat optimaalisesti eikä kukaan saa taktista etua toista vastaan. Jos jollain kilpailijalla on isoimmat lihakset, niin se vie todennäköisimmin voiton. Mutta jos kilpailun ”lihaskimppu” ei pelaa taktisesti optimaalisesti, voi voimiltaan heikompi kääntää edun itselleen hyvällä peliteorian ymmärryksellä. Parhaiten peliteorian oppeja on otettu käytäntöön yritystalouden kilpailutilanteissa, mutta myös esim. menestyvät pokerinpelaajat käyttävät Nashin tasapainoa apuna pelistrategiaa pohtiessaan.
Peliteorian mahdollisuudet lentopallossa
Peliteorian oppeja voi kuitenkin soveltaa moniin urheilulajiin ja lentopallo on tästä erittäin hyvä esimerkki. Mietitään seuraavaa yksinkertaisettua tilannetta (kts. kuva):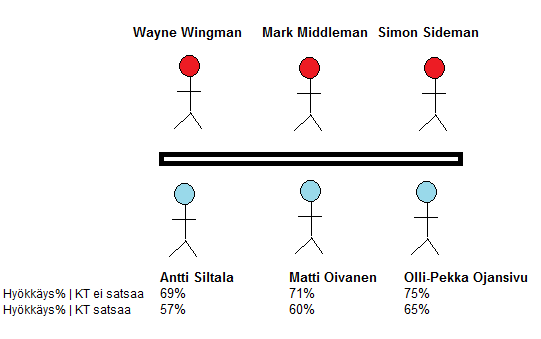
Hyökkäävä joukkue, Sininen:![]()
![]()
-Passari voi passata kolmeen paikkaan: 2-paikkaan Olli-Pekalle, keskelle Matille tai 4-paikkaan Antille. Oletuksena on, että takana 6-paikalla oleva pelaaja on tehnyt noston heittäytyen eikä ole hyökkäysvalmiudessa.
Torjuva joukkue, Punainen:
– Laitatorjujat torjuvat aina omaa laitaansa
– Keskitorjuja Mark voi joko
- Jäädä keskelle odottamaan mahdollista keskihyökkäystä
- Aavistaa hieman Simonin avuksi Olli-Pekkaa vastaan tai
- Aavistaa hieman Waynen avuksi Anttia vastaan
Kuvassa näkyvät kaikille hyökkääville pelaajille tähän nimenomaiseen tilanteeseen liittyvät hyökkäystehoprosentit (todennäköisyys, että pallo päättyy oman joukkueen voittoon, jos pelaaja saa passin) kahdessa eri tapauksessa:
- Vastustajan keskitorjuja satsaa johonkin muuhun pelaajaan (isommat prosentit)
- Vastustajan keskitorjuja satsaa juuri häneen (pienemmät prosentit)
Oletetaan myös, että molempien joukkueiden tilastovalmentajilla on kattavat tilastot, joiden perusteella molempien joukkueiden valmentajat tietävät kuvassa esitetyt hyökkäystehoprosentit kaikille hyökkääjille. Tästä eteenpäin pelin voidaan olettaa olevan hyökätessä oman joukkueen pallonvoittotodennäköisyyden maksimointia ja puolustaessa vastustajan pallonvoittotodennäköisyyden minimointia.
Taktiikan kehitys
- Hyökkäävän Sinisen joukkueen aluksi hyvin yksinkertaisesti ajatteleva valmentaja käskisi passarin passata aina tässä tilanteessa Olli-Pekalle, koska sillä on parhaat tehoprosentit.
- Kun näin tapahtuu monta kertaa peräkkäin, Punaisen valmentaja huomaa toistuvat passit Olli-Pekalle ja käskee keskitorjuja Markin mennä aina Simonin avuksi pitämään Olli-Pekkaa.
- Kun Sinisen valmentaja huomaa tämän, hän järkeilee, ettei Olli-Pekalle enää kannata kokoajan passata. Olli-Pekan hyökkäyprosentti (65%) on vähemmän kuin esim. Matin (71%) oletuksella, että keskitorjuja Mark aavistaa aina Olli-Pekan kimppuun. Ratkaisuksi tähän hän käskee passarin aina satunnaisesti passata 50% ajasta Olli-Pekalle ja 50% ajasta Matille.
- Kun Punaisen valmentaja huomaa tämän taktiikkamuutoksen, tajuaa hän että Mattiakin on pidettävä kiinni, ettei hän pääsisi tekemään pisteitä lähes vapaalta verkolta. Niinpä hän käskee Markia jatkossa satsaamaan satunnaisesti jatkossa 50% ajasta Mattiin ja 50% ajsta Olli-Pekkaan.
- Tässä tilanteessa pystymme esim. Excelillä laskemaan siniselle pallonvoittotodennäköisyydeksi 67.8%. Nyt Sinisen tilastovalmentaja huomaa, missä mennään: molempien joukkueiden taktiikat huomioiden Sinisen pisteen todennäköisyys on 67.8%, mutta Antti voittaisi pallot 69% todennäköisyydellä nyt kun keskitorjuja jättää hänet aina rauhaan (samoin kun John Nashin opiskelukaverit jättivät toiseksi kauniimman naisen rauhaan). Kannattaisikohan Antillekin välillä passata?
Kohti tasapainoa
Jos edellisessä kappaleessa kuvattua valveentuneiden valmentajien (tilastovalmentajien avustuksella) käymää taktiikoiden ja vastataktiikoiden säätämistä jatkettaisiin loputtomiin, päädytään jossain vaiheessa ns. tasapainotilaan. Tällöin kumpikin joukkue pelaa sellaisella taktiikalla, jota vastaan vastustaja ei voi enää saada lisäetua muuttamalla taktiikkaa. Kiitos John Nashin, pystymme tämän tasapainotilan laskemaan. Tässä tapauksessa se olisi seuraava:
| Wayne Wingman | Mark Middleman | Simon Sideman | |
|---|---|---|---|
| Torjunnan tasapainojakauma: | 7% | 25% | 68% |
| ———————– | ———————– | ———————– | |
| Passien tasapainojakauma: | 30% | 33% | 37% |
| Antti Siltala | Matti Oivanen | Olli-Pekka Ojansivu |
Tämä tarkoittaa, että passari valitsee satunnaisesti passin suunnan niin, että 30% todennäköisyydellä passi menne Antille, 33% todennäköisyydellä passi menee Matille ja 37% todennäköisyydellä passi menee Olli-Pekalle. Toisaalta Mark aavistelee 7% ajasta Antin suuntaan, 68% ajasta Olli-Pekan suuntaan ja 25% ajasta jää odottamaan passia keskelle. Käytännössä tällainen pelitaktiikka pitäisi toteuttaa pesäpallosta tutun merkkiviuhkan kanssa: tilastovalmentaja arpoo seuraavan siirron tietokoneella tilanteeseen sopivasti painotetulla satunnaisgeneraattorilla ja näyttää salaisen merkin pelaajille.
Kun pelaajat pelaavat tasapainon mukaisesti, niin näissä tilanteissa Sininen voittaa pallon 68.2% todennäköisyydellä.
Onko Nashin tasapaino optimaalinen pelitapa?
Vastaus otsikon kysymykseen: ei välttämättä. Tasapainon mukaan pelaaminen varmistaa sen, ettei vastustaja voi saada taktista etua joukkuettamme vastaan. Näin ollen se on paras lähtökohta kun vastassa on taktisesti valveutunut joukkue. Mutta jos vastustaja poikkeaa tasapainosta ja me tiedetään se, niin meidänkin kannattaa adjustaa taktiikkaa vastustajan mukaan. Palataan esimerkissämme taktiikan kehityksessä kohtaan 4. ja oletetaan nyt Punaisen valmentajaksi tilastoista piittaamaton jääräpää. Hän käskee Markin keskittyä aina vain Mattiin ja Olli-Pekkaan. Nyt Sininen joukkue saa taktiikalla ”ilmaisen lounaan” passaamalla aina Antille: tasapainotaktiikan 68.2% muuttuu nyt 69%:ksi.
Kurkistus todellisuuteen
 John Nash aikanaan sairastui skitsofreniaan matemaatikon uransa aikana. Yritetään me kuitenkin vielä pitää ajatukset lähellä todellisuutta. On selvää että esitettyssä esimerkissä on jouduttu tekemään monia yksinkertaistuksia todellisiin tilanteisiin verrattuna. Prosenttien kymmenyksen verran laskimen näytöllä etua tuovat taktiikka-muutokset ovat käytännön epävarmuuksista johtuen yhtä tyhjän kanssa. Tärkein tapa kehittää joukkueen peliä on edelleen harjoituttaa hyökkäystaitoja, jotta omat tehoprosentit nousee ja harjoittelemalla puolustamista, jotta vastustajan tehoprosentit laskee. Jos kuitenkin vastustajalle antaa useita prosenttiyksikköjä ylimääräistä taktista etua joka pallossa niin varmasti se näkyy myös ottelun lopputuloksessa. Peliteorialla olisi varmasti annettavaa monille lentopallojoukkueille, vaikkei sitä prosentin kymmenyksien tarkkuudella pystyisikään toteuttamaan.
John Nash aikanaan sairastui skitsofreniaan matemaatikon uransa aikana. Yritetään me kuitenkin vielä pitää ajatukset lähellä todellisuutta. On selvää että esitettyssä esimerkissä on jouduttu tekemään monia yksinkertaistuksia todellisiin tilanteisiin verrattuna. Prosenttien kymmenyksen verran laskimen näytöllä etua tuovat taktiikka-muutokset ovat käytännön epävarmuuksista johtuen yhtä tyhjän kanssa. Tärkein tapa kehittää joukkueen peliä on edelleen harjoituttaa hyökkäystaitoja, jotta omat tehoprosentit nousee ja harjoittelemalla puolustamista, jotta vastustajan tehoprosentit laskee. Jos kuitenkin vastustajalle antaa useita prosenttiyksikköjä ylimääräistä taktista etua joka pallossa niin varmasti se näkyy myös ottelun lopputuloksessa. Peliteorialla olisi varmasti annettavaa monille lentopallojoukkueille, vaikkei sitä prosentin kymmenyksien tarkkuudella pystyisikään toteuttamaan.
Tämä kirjoitus on kirjoitettu yhdessä Mestaruusliigan ex-tilastovalmentaja Johannes Ärjen kanssa. Esimerkissä käytettyjen pelaajien nimet ja niihin liittyvät hyökkäystehoprosentit ovat keksittyjä. Jos jollakin todellisella pelaajalla on sama nimi, niin se on puhdasta sattumaa. Voit kokeilla itse laskea tasapainojakaumia erilaisiin tilanteisiin Ärjen tekemällä laskurilla.
